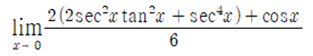(송두원T)
안녕하세요. 튜나편입에서 수학을 가르치고 있는 송두원T입니다. 오늘은 편입 수학을 공부하는 학생들이 가장 많이 하는 실수이자, 가장 먼저 바로잡아야 할 ‘마음가짐’에 대해 이야기해 보려 합니다.
이 글의 제목은 ‘수학 공부가 아닌 편입수학 공부를 하자’입니다. 이 차이를 아는 것이 여러분의 1년, 그리고 합격의 결과를 결정할 것입니다.
‘수학’이 아닌 ‘편입수학’을 공부해야 하는 이유 (feat. 로피탈의 함정)
[편입수학 공부법 / 편입수학 방향성 / 수능수학과의 차이점]
🚨 가장 큰 실수: 고등학교 때의 습관을 버리지 못하는 것
많은 학생들이 편입수학을 시작할 때, 고등학교 때 문제를 풀던 습관과 방식을 그대로 적용하려 합니다. 하지만 이것은 매우 좋지 않은 공부 방법입니다.
저희는 수학자가 아니라, ‘입시’라는 시험을 준비하는 입시생입니다. 모든 입시 시험에는 그 시험이 원하는 ‘방향성’이 존재합니다. 수능이 원하는 문제 풀이와 편입이 원하는 문제 풀이는 분명히 다릅니다. 이 방향성부터 제대로 잡아야 합니다.
무슨 소리인지, 실제 예시를 통해 극명하게 보여드리겠습니다.
CASE STUDY: 로피탈의 함정 vs 매클로린 급수
아래와 같은 극한 문제가 있다고 가정해봅시다.
이 문제를 보고 많은 학생들이 ‘로피탈 공식’을 떠올립니다. 하지만 이 문제를 편입 시험장에서 로피탈을 사용해 푼다면 어떻게 될까요?
❌ 잘못된 접근: 수능식 풀이 (로피탈)
이 문제를 로피탈 정리로 풀기 위해서는, 분자/분모를 **무려 3번이나 미분**해야 답이 나옵니다. 곱미분이 계속 사용되어 계산 과정이 매우 복잡하고, 실수할 가능성이 높으며, 최소 5분 이상의 시간이 소요될 수 있습니다. 수능이라면 사고력을 보여줄 수 있겠지만, 편입에서는 아닙니다.
✅ 올바른 접근: 편입식 풀이 (매클로린 급수)
편입 시험에서 이 문제는 “당신, 대학 1~2학년 과정인 ‘매클로린 급수’를 제대로 암기하고 있습니까?”를 묻는 문제입니다. 매클로린 급수 공식을 사용하면, 미분 과정 없이 **단 10~20초 안에** 암산으로도 풀이가 가능합니다. 심지어 워낙 자주 출제되는 유형이라, 답 자체를 **’1/2’**로 외워버리는 방법도 있습니다.
이것이 바로 ‘수학 공부’와 ‘편입수학 공부’의 차이입니다. 편입 시험은 1, 2학년 수준의 **지적 능력, 암기 능력, 문제 풀이 속도, 순발력**까지 모두 평가하는 시험입니다. “이게 무슨 수학이에요, 답을 외우라니요…”라는 반응이 나올 수 있습니다. 하지만 우리는 편입이라는 입시에 성공하기 위해, 그 시험이 원하는 방향성을 반드시 따라가야 합니다.
오늘의 결론
미적분부터 잘못된 방향성으로 공부하면, 앞으로 배울 선형대수, 다변수, 공수 모두에서 무너지게 됩니다. 고등학교 때의 공부법을 과감히 버리세요. 우리는 수학자가 아니라, 입시에 성공해 원하는 학교에 입학하는 것이 목표입니다.
그 목표를 위해서는, 문제 하나 더 외워가는 것이 이득입니다.
“편입을 경험했기에, 합격은 튜나입니다.”