(송두원T)
안녕하세요. 튜나편입에서 수학을 가르치고 있는 송두원T입니다. 오늘은 편입수학의 중요한 한 축인 ‘선형대수학’에 대한 이야기를 해볼까 합니다. 미적분학이라는 큰 산을 넘고 나면, 많은 학생들이 가우스-조르단, Rank, 고유값, 고유벡터 등 무척이나 생소한 개념들의 등장에 당황하곤 합니다.
그래서 이번 시간에는 선형대수학의 시작에 서 있는 여러분들을 위해, 이 과목의 궁극적인 목표는 무엇인지, 그리고 우리가 왜 이 개념들을 배워야만 하는지 이야기해 보겠습니다.
편입수학 ‘선형대수학’ 시작하기 (feat. 행렬, 벡터, 선형조합)
[선형대수학 / 편입수학 공부법 / 행렬과 벡터 / 송두원T 칼럼 1편]
🤔 선형대수학, 왜 배울까요?
여러분이 편입에 성공하여 공대에 진학한다면, ‘선형대수’는 전공필수 과목으로 다시 만나게 될, 매우 중요한 학문입니다. 하지만 의문이 들 겁니다. “그렇게 중요하다면서, 왜 고등학교 수학에서는 ‘행렬’ 단원이 사라졌을까요?”
그 이유는 ‘제대로 활용할 수 없었기’ 때문입니다. 행렬은 벡터의 집합이자, 벡터를 표현하는 또 다른 방법입니다. 따라서 벡터를 배우지 않으면 행렬을 완전히 이해할 수 없습니다. 과거 문이과 공통과정에서 벡터를 배우지 않는 문과생들을 위해 ‘행렬’의 겉핥기식 개념만 가르치다 보니, 결국 고등학교 수학에서 그 자취를 감추게 된 것입니다.
이제 우리는 대학 수학으로서, 이 강력한 도구인 ‘선형대수학’의 진짜 의미를 마주할 시간입니다.
🎯 같은 문제, 3가지 다른 관점: 연립방정식 풀이
선형대수학의 힘을 이해하기 위해, 우리에게 아주 익숙한 연립방정식을 세 가지 다른 방법으로 풀어보겠습니다.
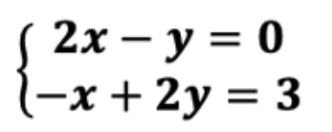
방법 1: 소거법 (중학생도 아는 방법)
가장 간단한 방법입니다. 두 번째 식에 2를 곱해 첫 번째 식과 더하면 변수 y가 사라지죠. 이를 통해 우리는 해가 x=1, y=2임을 쉽게 알 수 있습니다.
방법 2: 그래프 (고등학생의 관점)
두 개의 방정식은 각각 x-y 평면 위의 ‘직선’을 나타냅니다. 따라서 두 직선이 만나는 ‘교점’을 구하면 그것이 바로 연립방정식의 해가 됩니다.
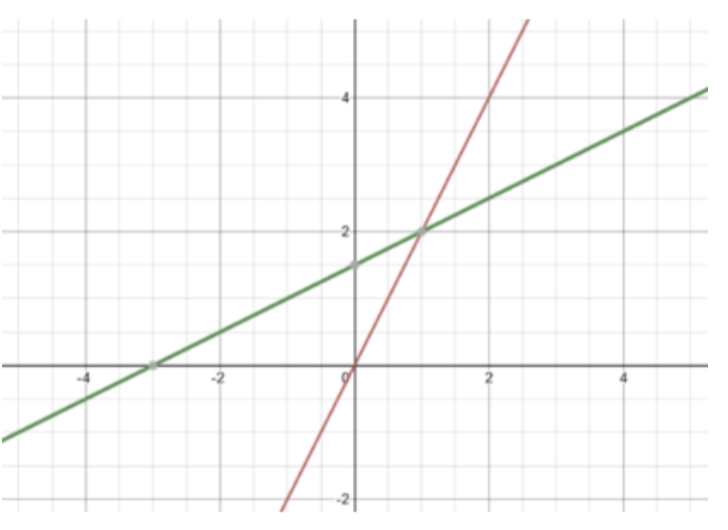
그래프에서 보듯, 교점의 좌표는 정확히 (1, 2)입니다. 방법 1과 동일한 결과죠.
방법 3: 선형조합 (대학생, 바로 당신의 관점!)
이제 선형대수학의 세계로 들어갑니다. 우리는 더 이상 식을 가로(행)로 보지 않습니다. 세로(열)로, 즉 ‘각 변수에 대한 조합’으로 식을 바라봅니다.
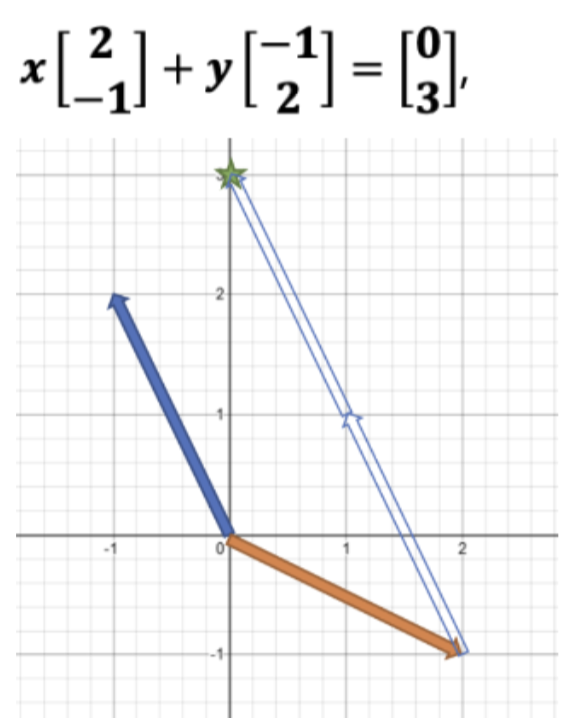
이것은 “주황색 벡터와 파란색 벡터를 몇 배씩 더해야 녹색 별(목표 지점)에 도달할 수 있는가?”라는 질문과 같습니다. x는 주황색 벡터를 늘리는 배수, y는 파란색 벡터를 늘리는 배수입니다. 그림으로 보면, 주황색 벡터를 1배, 파란색 벡터를 2배만큼 더했을 때 정확히 녹색 별에 도달합니다. 따라서 해는 역시 x=1, y=2입니다.
🚀 그래서, 왜 굳이 어렵게 풀어야 할까?
쉬운 연립방정식을 뭐하러 이렇게 어렵게 푸냐고 반문할 수 있습니다. 하지만 변수가 3개(x, y, z)가 되면 어떨까요? 변수가 100개라면요?
그래프를 그리는 방법은 3차원을 넘어서는 순간 막히지만, 선형대수학의 ‘선형조합’ 방식은 변수가 몇 개가 되든 동일한 원리로, 컴퓨터를 통해 순식간에 해를 찾아낼 수 있습니다. 이것이 바로 우리가 선형대수학을 배우는 이유입니다.
[클릭] 다음 편 바로 읽으러가기…!
오늘 글이 좀 어렵게 느껴지셨나요? 괜찮습니다. 중요한 것은 연립방정식을 ‘선형대수학’의 관점으로 풀 수 있다는 사실을 아는 것입니다. 다음 2편에서는 선형대수학의 꽃, ‘고유값’과 ‘고유벡터’에 대한 고찰로 찾아뵙겠습니다!


