안녕하세요~~
오늘은 다시 푸리에 급수에 대해 마저 말씀드릴거예요.
하지만, 편입 시험의 범위에서 조금 벗어난 얘기입니다.
어렵지 않게, 푸리에 급수를 사용하는
진정한 이유에 대해 말씀드리겠습니다.
우선, 푸리에 급수의 기저함수로
삼각함수가 사용됨으로써 얻는 가장 큰 장점은
주기성과 더불어 삼각함수의 직교성을 이용할 수 있다는 겁니다.
직교성은 이용할 수 있다는 것은 곧 벡터의 계산으로,
다름아닌 선형 대수로 표현할 수 있다는 것이지요!!
공업 수학 진도상 선형 대수가 먼저 등장하고,
선형 대수는 무척 간단하게 훑고 넘어가기 때문에
사실 여러분은 이 말을 이해하기 힘들거예요.
하지만 앞서 잠깐 언급한 고속푸리에변환(FFT)을 비롯해
여러 푸리에 관련 변환식은 선형대수를 이해했을 때
비로소 그 진가가 나타나게 됩니다.
분명, 편입에 성공하신 이후 전공 과목에서 배우실 테니
그때쯤 어디선가 이런 소릴 들어봤는데? 하고 기억해주세요 ㅎㅎ
또한 편입 수학 범위에서도 복소 푸리에 급수가 등장하지요.
복소 푸리에 급수는 오일러 공식을 활용해 푸리에 급수를
복소수 형태, 지수 꼴로 변형한 녀석입니다.
오일러 공식은 다음과 같지요.

심지어는 다소 극단적인 형태,
사각/삼각 신호의 반복이거나 톱날 형태까지도
나타낼 수 있습니다.
바로 다음과 같이요.

위 그림은 짧은 영상 중 신호가 분리되던 순간을 나타낸 겁니다.
이 그림에서부터 설명을 드릴게요.
빨간 그래프가 우리가 보는 신호입니다!
시간에 따른 신호 크기예요. 시간 영역입니다.
저런 이빨 모양의 신호들도 우리는 여러 삼각함수의 합으로
나타낼 수 있다!! 이것이 방금까지 설명 드린 푸리에 급수였지요?
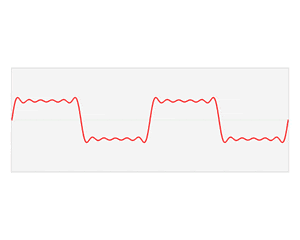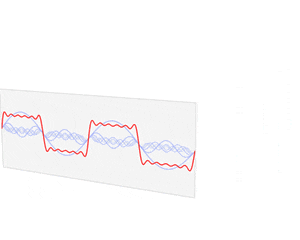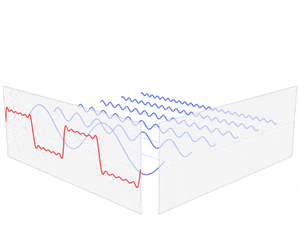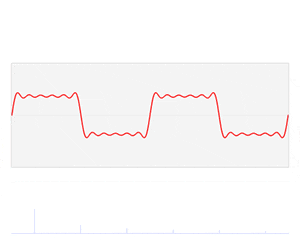
그 내용이 빨간 그래프 뒤에 나열된 파란 삼각함수들입니다.
파란 삼각함수들을 모두 더하면, 놀랍게도
빨간 이빨모양 그래프를 얻을 수 있어요.
자, 그럼 우측의 직선 몇 개만 그려진 횡한 그래프는 무엇일까요?
이 그래프는 바로 삼각함수들의 주파수와 진폭을 표현하고 있습니다.
바로 주파수 영역에서 말이지요.
이렇게 같은 신호, 같은 물리적 현상을
다르게 표현할 수 있습니다.
그 관점을 다르게 해서 말이예요!!
이것이 바로 푸리에 급수를 통해 우리가 하려고 하는 겁니다.
시간 영역의 이빨 모양 그래프를 다시 봐 보세요.
여러분은 저 그래프를 보고, 어떠한 함수들의 합으로 이루어 졌는지
그 함수들의 특징은 무엇인지 알 수 있나요?
하지만 주파수 영역의 그래프를 보면,
어떤 특징을 지닌 함수들로 구성되어 있는지 바로 알 수 있습니다.
각종 신호와 주기적 물리량의 해석에
푸리에 급수가 사용되는 이유가 바로 이것입니다.
그 구성 성분들을 알아보기 위함이예요.
다소 이해가 어렵나요?
하지만 너무 겁먹지 마세요.
다시금 말씀드리지만, 편입 수학 시험에서는
본질적인 이러한 해석은 시험 범위가 아닙니다!
단순히 푸리에 급수 계산식을 적용하고
풀어낼 수 있느냐?! 까지가 편입 시험 범위예요.
하지만 복잡한 삼각함수 전개식들을
무조건 외우고 있는 여러분께
도대체 이걸 어디에 쓰는 것이고 왜 배우는 것인가를
조금이나마 말씀드리고 싶었어요.
다음 시간에는 푸리에 변환에 대해 말씀드리겠습니다.
그럼 안녕히계세요.
감사합니다~~

