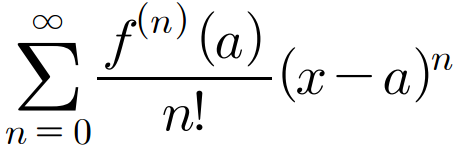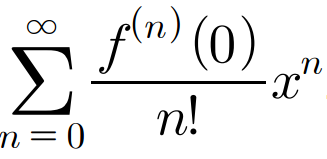안녕하세요. 튜나편입에서 수학을 가르치고 있는 송두원T입니다. 편입수학을 공부하다 보면, 이게 수학인지 암기 과목인지 헷갈릴 때가 많습니다. 하지만 제가 편입을 준비할 때, ‘매클로린 급수’라는 단원을 배우며 수학의 신비로움과 수학자들에 대한 경외심을 느꼈습니다. 입시 공부에 찌든 저에게 신선한 충격을 주었죠.
그래서 오늘은, 여러분도 저와 같은 신선한 충격을 받으실 수 있도록
아주 쉽게 매클로린 급수에 대해 이야기해 보겠습니다!
편입수학,
매클로린 급수의 신비 (수포자도 이해하는 개념 유도)
[매클로린급수 / 테일러급수 / 편입수학 공식 / 송두원T 칼럼]
🤔 왜 수학자들은 ‘다항함수’를 사랑할까?
함수에는 여러 종류가 있지만, 대표적으로 ‘다항함수’와 ‘초월함수’가 있습니다. 다항함수는 상대적으로 계산도, 이해도 쉬운 ‘착한’ 함수입니다. 반면, 삼각함수($\sin x$), 지수함수($e^x$), 로그함수($\ln x$) 같은 초월함수들은 이름부터 뭔가 싸늘하죠?
그래서 위대한 수학자들은 늘 고민했습니다. “이해하기 어려운 저 초월함수들을, 우리가 잘 아는 ‘다항함수’라는 언어로 번역할 수는 없을까?” 하고 말이죠.
✨ 초월함수를 번역하는 마법: 테일러 급수와 매클로린 급수
수많은 초월함수를 다항함수 꼴로 나타내기 위한 획기적인 방법, 그것이 바로 ‘테일러 급수’입니다. 고등학교 때는 본 적 없는, 대학 수학의 개념이죠.
지금 위 식이 이해되지 않아도 괜찮습니다. 간단히 말해, 테일러 급수는 **모든 초월함수를 다항함수로 표현하는 마법 같은 번역기**라고 생각하시면 됩니다.
그리고 오늘 우리가 탐험할 ‘매클로린 급수’는 이 테일러 급수의 아주 특별하고 중요한 ‘스페셜 에디션’입니다.
매클로린 급수란, 테일러 급수에서 기준점
a를0으로 설정한, 더 간단하고 아름다운 형태의 급수입니다.
🔬 지수함수 e^x 매클로린 급수, 직접 유도해보기
그렇다면 대체 어떻게 초월함수를 다항함수로 표현할 수 있을까요? 가장 대표적인 지수함수 $e^x$를 통해 그 신비로운 과정을 함께 따라가 보겠습니다.
STEP 1: “만약 $e^x$가 다항함수라면?” 가정하기
먼저, $e^x$를 무한한 차수의 다항함수로 표현할 수 있다고 가정해봅시다. 그럼 아래와 같은 형태로 쓸 수 있겠죠?
🖼️ $e^x = a + bx + cx^2 + dx^3 + \dots$ ( ‘지수함수를 다항함수로 가정하는 식’)
이제 우리의 목표는 미지의 계수 $a, b, c, d, \dots$ 를 찾아내는 것입니다.
STEP 2: 양변에 x = 0 대입하기 (상수항 a 구하기)
위 식은 항등식이므로, 양변에 똑같이 $x=0$을 대입해도 등호는 성립합니다.
🖼️ $e^0 = a + 0 + 0 + \dots$ (alt: ‘x=0을 대입하는 과정’)
$e^0=1$이므로, 우리는 첫 번째 계수 a = 1 을 찾아냈습니다!
STEP 3: 미분하고, x = 0 대입하기 (계수 b, c, d… 구하기)
이제 나머지 계수를 찾기 위해 ‘미분’을 활용합니다. $e^x$는 미분해도 그대로 $e^x$라는 점을 이용하는 것이죠. 원래 식의 양변을 미분해봅시다.
🖼️ $(e^x)’ = (a + bx + cx^2 + \dots)’ \implies e^x = b + 2cx + 3dx^2 + \dots$ (alt: ‘양변을 미분하는 과정’)
이 상태에서 다시 양변에 $x=0$을 대입하면? 좌변은 $e^0=1$, 우변은 $b$만 남습니다. 즉, b = 1 입니다! 이 과정을 계속 반복합니다.
STEP 4: 규칙성 발견과 공식 완성! (팩토리얼의 등장)
이 미분과 대입을 반복하면, 계수들은 아래와 같은 값을 갖게 됩니다.
🖼️ $a = 1, b = 1, c = 1/2, d = 1/6, e = 1/24, \dots$ (alt: ‘계수 값들의 나열’)
분모에 있는 숫자들, 1, 2, 6, 24… 뭔가 규칙이 보이지 않나요? 바로 팩토리얼(factorial, !)입니다! ($1=1!, 2=2!, 6=3!, 24=4!$)
결국, 우리는 $e^x$를 아래와 같은 아름다운 다항함수 꼴로 변환하는 데 성공했습니다. 이것이 바로 $e^x$의 매클로린 급수입니다.
🖼️ $e^x = 1 + x + \frac{x^2}{2!} + \frac{x^3}{3!} + \dots = \sum_{n=0}^{\infty} \frac{x^n}{n!}$ (alt: ‘지수함수 e의 x승의 매클로린 급수 공식’)
개념 이해부터 문제 풀이까지, 가장 완벽한 로드맵
매클로린 급수처럼 어려운 개념도, 올바른 방향으로 이끌어주는 멘토와 함께라면 즐거운 탐구가 될 수 있습니다. 튜나편입의 **’영어 x 수학 프리미엄 올인원 과외’**는 당신의 모든 수학적 질문에 답해드립니다.
이처럼 복잡해 보이는 초월함수도 미분과 0이라는 단순한 도구를 통해, 규칙적인 다항식으로 변신할 수 있습니다. 이런 개념들에서 수학적인 호기심과 재미를 느껴야, 힘들고 긴 수험 생활을 버텨낼 작은 원동력이 되지 않을까 생각합니다. 긴 글 읽어주셔서 감사합니다.