안녕하세요. 튜나편입에서 수학을 가르치고 있는 송두원T입니다. 오늘은 미적분학의 심장, ‘미적분학의 기본 정리’에 대해 이야기해 볼까 합니다. 수많은 미적분 공식을 통달한 여러분도 막상 이 정리의 이름을 들으면 ‘그런 게 있었나…?’ 싶을 겁니다.
하지만 여러분은 이미 매일 이 위대한 정리를 사용하고 있습니다.
오늘은 그 익숙함 속에 숨겨진 위대한 원리를 함께 파헤쳐 보겠습니다. 어렵지 않으니 잘 따라와 주세요!
편입수학,
‘미적분학의 기본정리’가 뭐길래?
(수포자 필독)
[미적분학의 기본정리 / 정적분 / 미분과 적분 관계 / 편입수학]
🤔 STEP 1: 모든 것은 ‘넓이’를 구하려는 노력에서 시작됐다
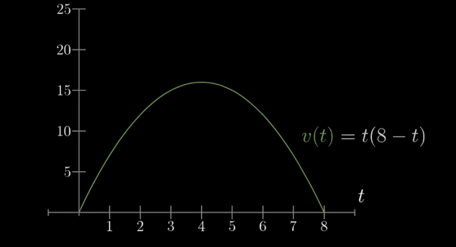
미적분의 시작은 ‘변화하는 무언가’를 관찰하는 것입니다. 가장 대표적인 예시로, 시간에 따라 속도가 변하는 자동차의 이동 거리를 구하는 문제를 생각해봅시다.
8초 동안 자동차가 이동한 거리는 위 그래프의 아래쪽 넓이와 같습니다. (시간 x 속도 = 거리) 하지만 곡선으로 둘러싸인 부분의 넓이는 어떻게 구해야 할까요? 수학자들은 우리가 아는 ‘직사각형’으로 근사치를 구하는 방법을 생각했습니다.
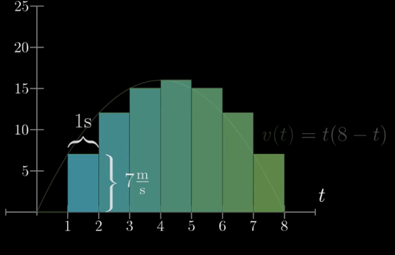
구분구적법: 잘게 쪼개어 더한다!
그래프 아래를 수많은 얇은 직사각형으로 나누어 그 넓이를 모두 더하는 것입니다. 하지만 그림에서 보듯, 직사각형으로만은 정확한 넓이를 구할 수 없습니다. 오차가 발생하죠.
이 오차를 줄이려면 어떻게 해야 할까요? 맞습니다. 직사각형의 가로 길이를 0.5초, 0.1초, … , 0.000001초처럼 거의 0에 가깝게, 무한히 잘게 쪼개면 됩니다. 이것이 바로 ‘극한’의 개념이며, 이렇게 오차를 줄여나가는 과정이 바로 ‘정적분’의 시작입니다.
✨ STEP 2: 미분과 적분을 연결하는 위대한 다리
자, 이제 한 걸음 더 나아가 봅시다. 우리는 임의의 시간 T에 대해, 출발부터 T까지의 ‘누적 이동거리’를 나타내는 함수 s(T)를 구하고 싶습니다. 이 s(T)를 구하는 과정이 바로 미적분학의 기본 원리를 드러냅니다.
아주 짧은 시간 dT 동안의 이동거리를 ds라고 해봅시다. 이때의 속도 v(T)는 ds/dT, 즉 **’이동거리 함수 s(T)의 순간 변화율(미분계수)’**과 같습니다. 이 말은 곧, 우리가 모르는 이동거리 함수 s(T)를 미분했더니 속도 함수 v(t)가 되었다는 뜻입니다!
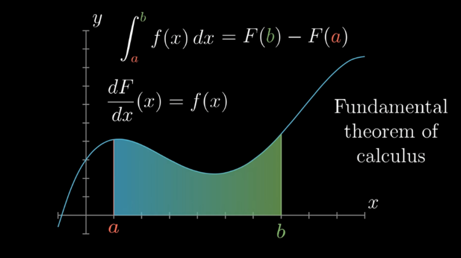
결국, 속도 그래프 아래의 넓이를 구해 이동거리를 알아내는 ‘적분’ 문제는, ‘미분해서 속도 함수가 되는 원래 함수(원시함수)를 찾는’ 문제와 같아집니다. 이것이 바로 미분과 적분을 연결하는 위대한 다리, **미적분학의 기본정리**입니다.
오늘의 결론
수학에서는 덧셈과 뺄셈, 곱셈과 나눗셈, 지수와 로그처럼 서로 쌍을 이루는 ‘역연산’ 관계가 존재합니다. 미분과 적분도 마찬가지입니다. 미분의 역과정이 적분으로 정의되는 이 기본 원리를 이해하는 것이, 복잡하고 신기하게 생긴 함수들의 적분 문제를 해결하는 첫걸음입니다.
“편입을 경험했기에, 합격은 튜나입니다.”