(송두원T)
안녕하세요. 튜나편입에서 수학을 가르치고 있는 송두원T입니다. 이전 칼럼들이 다소 어렵게 느껴지셨을 분들을 위해, 오늘은 모든 것의 시작인 ‘기초수학’에 대해 이야기해보려 합니다. “선생님이 얘기하는 고교 수학, 기초수학 자체를 모르겠다고!” 외치는 분들이 계실 겁니다.
괜찮습니다. 흘리고 계신 눈물과 손에 쥔 죽창을 잠시 내려놓으시길 바라며, 완전 노베이스 여러분을 위해 편입 수학을 어떻게 시작해야 하는지, 그 첫걸음을 함께 떼어보겠습니다.
수포자를 위한 편입수학 시작 가이드 (feat. 기초수학의 모든 것)
[편입수학 노베이스 / 기초수학 / 편입수학 공부법 / 송두원T 칼럼]
🚀 STEP 1: 부끄러움을 버려라
편입 수학을 목표로 하고 가장 먼저 해야 할 일은, 다름 아닌 ‘부끄러움을 버리는 일’입니다. 배움에 있어 자신이 ‘모른다’는 것을 인정하는 일은 결코 쉽지 않습니다. 하지만 ‘모르고 있다’는 사실을 정확히 아는 것부터 모든 공부의 시작이 됩니다.
스스로 ‘노베이스’라고 생각하기에 앞서, 본인의 실력을 객관적으로 파악해야 합니다. 이를 위해 튜나편입에서는 수학 기초 테스트를 제공하고 있습니다. 자기객관화가 덜 된 학생들은 꼭 테스트를 먼저 보시길 바랍니다.
이 글은 미적분이 기억나지 않는 수준을 넘어, 미분 기호 자체가 초면이라 수줍은 분들을 위한 이야기입니다. 아무런 바탕 없이 $x^2$을 미분하면 $2x$가 된다는 공식을 암기하는 것은 쓸모없는 짓입니다. 부끄러움을 떨치고, 모든 수학의 근간인 ‘고1 수학’ 과정에 주목해야 합니다.
🏛️ STEP 2: 모든 수학의 근간, 고1 수학 정복하기
고1 수학은 우리가 문·이과를 선택하기 이전, 모두가 함께 공부했던 수학의 뿌리입니다. 편입 수학에서 다루는 고1 수학의 핵심 목차는 다음과 같습니다.
물론 다 중요하지만, 편입 시험에 집중해봅시다. 수학 (하) 부분의 집합과 명제, 경우의 수는 편입 수학과 거의 관련이 없으므로, 이 부분은 과감히 넘어가셔도 마음이 편합니다.
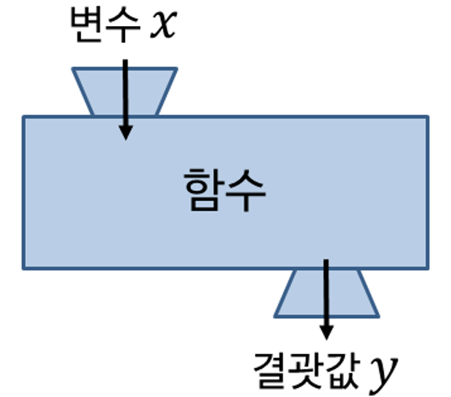
방정식과 함수, 그 근본적인 차이
많은 학생들이 방정식과 함수의 차이를 명확히 말하지 못합니다. 이것은 매우 중요합니다.
- 방정식: 미지수를 포함한 등식입니다. 식을 ‘참’이 되게 하는 미지수(해)를 구하는 것이 목표입니다. (예: $x-1=0 \implies x=1$)
- 함수: 두 변수 사이의 ‘대응 관계’입니다. 입력(x)에 따라 일정한 규칙을 거쳐 결과(y)가 나오는 것이 핵심입니다. (예: $y=x-1$)
함수는 이 대응 관계를 ‘그래프’로 시각화할 수 있다는 강력한 차이가 있습니다. 그리고 함수의 결과값인 y가 0이 되는 지점이 바로, 방정식의 ‘해’가 되는 것이죠. 이 관계를 이해하는 것이 수학적 이해의 핵심입니다.
도형의 방정식과 함수
도형의 방정식에서는 주로 직선과 원을 다룹니다. 고등학교 때 원과 직선 사이의 최소 거리를 구하는 문제를 ‘판별식’으로 풀었죠? 하지만 이 모든 최대/최소 문제는 사실 ‘미적분’ 문제입니다. 나중에 미적분을 배우고 돌아보면 훨씬 쉽게 풀어낼 수 있습니다. 또한, 원의 방정식은 이후 지겹도록 만날 삼각함수와 밀접한 연관이 있으니 꼭 기억해주세요.
함수 단원에서는 유리함수, 무리함수 등을 배우지만, 우리에게 더 중요한 것은 앞으로 배울 편입수학 모든 과목의 기반이 되는 ‘함수’라는 개념과 사용법을 정확히 파악하는 것입니다.
결론: 기초부터, 차근차근
오늘 살펴본 고1 수학 내용들은, 앞으로 배울 미적분 과정에서 계속해서 자연스럽게 사용되고 복습되는 부분들입니다. 이 내용들이 있구나! 하고 이해하는 것만으로도, 이어지는 수학 공부에 훨씬 쉽게 적응할 수 있을 겁니다. 편입 수학은 결코 어렵지 않습니다. 기초수학부터 하루하루 공부해나가면 금세 실력이 늘어갈 거예요!