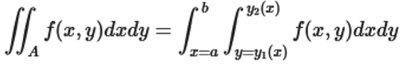(송두원T)
안녕하세요. 튜나편입에서 수학을 가르치고 있는 송두원T입니다. 오늘은 지난 시간 ‘편미분’에 이어, 다변수함수에서의 ‘다중적분’에 대해 이야기해 보겠습니다. 편미분이 미분의 확장판이었다면, 다중적분은 적분의 확장판입니다. 그리고 이 개념을 통해, 우리는 기상천외하게 생긴 3차원 도형의 부피를 구할 수 있는 강력한 무기를 얻게 됩니다!
편입수학, 다중적분(중적분) 완전 정복! (개념부터 실전 꿀팁까지)
[다중적분 / 중적분 / 편입수학 / 다변수 미적분학]
🤔 중적분이 뭔가요? (넓이에서 부피로의 차원 확장)
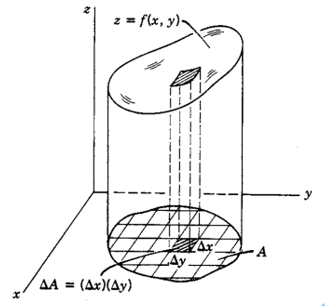
미적분의 기본 정리에서, ‘적분’이란 잘게 쪼갠 수많은 직사각형들의 넓이를 더하는 개념이라고 배웠죠? 다중적분(Multiple Integral), 그중에서도 이중적분(Double Integral, 중적분)은 이 개념을 3차원으로 확장시킨 것입니다.
즉, 얇은 ‘직사각형의 넓이’를 더하는 대신, 아주 가느다란 **’막대기의 부피’**를 차곡차곡 쌓아 올려 입체의 부피를 구하는 마법 같은 방법입니다. 이를 통해 우리는 기존의 회전체뿐만 아니라, 훨씬 더 괴이하고 복잡한 형태의 3차원 물체들의 부피를 정확하게 계산할 수 있게 됩니다!
🔑 중적분의 핵심: 적분 순서와 범위를 결정하는 법
중적분에서 가장 중요한 것은 바로 **’적분 구간’과 ‘적분 순서’를 설정**하는 것입니다. 이는 마치 레고 블록을 쌓을 때, 어떤 색 블록을 먼저, 어디서부터 어디까지 쌓을지 결정하는 것과 같습니다. 순서와 범위가 틀리면 전혀 다른 모양이 만들어지죠.
아래의 잘린 원기둥 예시를 통해 자세히 살펴보겠습니다.
예시: 잘린 원기둥의 부피 구하기
🖼️ 이곳에 ‘잘린 원기둥’ 예시 이미지를 추가하세요 (alt: ‘중적분 예시로 사용될 잘린 원기둥 3D 그래프’)
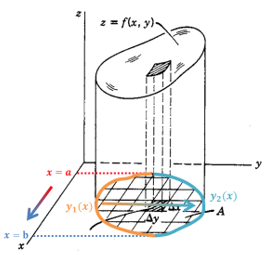
이 입체의 부피를 구하려면, 먼저 윗면을 아래의 x-y 평면에 그대로 눌러 찍어(정사영) 적분할 영역(R)을 정해야 합니다. 그림에서 x축의 범위는 $a$부터 $b$까지, y축의 범위는 함수 $y_1(x)$부터 $y_2(x)$까지입니다.
일반 정적분이 x를 $a$에서 $b$까지 변화시키며 넓이를 더했다면, 중적분은 **x를 $a$에서 $b$까지, y를 $y_1(x)$에서 $y_2(x)$까지 변화시키며 부피(막대기)를 쌓아 올린다**고 생각하면 쉽습니다. 이를 식으로 나타내면 다음과 같습니다.
가장 중요한 포인트!
같은 문제라도 x부터 적분할지, y부터 적분할지에 따라 계산 난이도가 하늘과 땅 차이로 달라질 수 있습니다. 어떤 순서로 적분해야 식이 더 간단해질지 판단하는 능력이 중적분 문제 풀이의 핵심입니다.
💡 실전! 중적분 문제 풀이 3가지 꿀팁
이론을 알았으니, 실전에서 써먹을 수 있는 팁을 알려드립니다.
- 적분 영역을 먼저 그려라: 문제가 주어지면, 가장 먼저 x-y 평면에 적분 영역(R)을 그려보세요. 영역의 모양을 보면 어떤 순서로 적분하는 것이 유리할지 직관적으로 파악할 수 있습니다.
- 적분 순서를 바꿔보라: 주어진 순서대로 적분을 시도했는데 계산이 너무 복잡하거나 불가능한 경우가 있습니다. 이때 적분 순서를 (dy dx → dx dy) 바꾸면 마법처럼 쉽게 풀리는 문제가 많습니다.
- 원형 영역은 극좌표를 의심하라: 적분 영역이 원이나 부채꼴 형태라면, 직교좌표보다 극좌표($r, \theta$)로 변환하여 푸는 것이 훨씬 간단하고 효율적입니다.
ㅎㅎ.. 좀 어려웠나요? 이 글을 읽는 시기에 따라 내용을 받아들이는 데 차이가 크겠지만, 언제가 되었든 다변수 미적분에서 가장 중요한 것을 콕 집어 이야기하라고 하면, **’적분의 순서와 범위에 유의하며 풀어나가야 한다’**입니다. 이 점 항상 신경 쓰며 문제 풀이를 해야 합니다!