(송두원T)
편입수학 ‘고계도함수’ 완전 정복
이름은 거창하지만, 알고 보면 정말 간단한 개념! 수학 자신감을 되찾아 가세요!
안녕하세요. 튜나편입에서 수학을 가르치고 있는 송두원T입니다. 이전 칼럼에서 다룬 미적분학의 기본 정리, 많이 어려우셨죠? ㅎㅎ 학생들이 너무 어려워하며 넘기셨을까 봐, 오늘은 조금은 쉽게 이해할 수 있는 ‘고계도함수’에 대해 이야기해 보려 합니다.
🤔 고계도함수, 이름만큼 어려울까?
‘고계도함수(Higher-order derivative)’는 이름만 들으면 무척 어려워 보입니다. 하지만 전혀 그렇지 않습니다. ‘도함수’는 미분을 통해 유도된 함수죠. 여기에 ‘높을 고(高)’ 자가 붙었으니, 그저 **”여러 번 미분을 통해 유도된 함수”**라는 뜻입니다. 한마디로, 해당 변수에 대해 여러 번 미분을 수행하면 그게 바로 고계도함수입니다!
단순히 계산을 여러 번 하는 것 이상의 의미를 파악하기 위해, 고계도함수의 의미와 편입 시험에서의 활용법까지 차근차근 알아보겠습니다.
🔢 1단계: 이계도함수 기호 완전 정복하기
가장 간단한 고계도함수인 ‘이계도함수(Second derivative)’부터 시작해봅시다. 이름에 숫자 2가 들어있죠? 맞습니다. **두 번 미분해서 유도된 함수**입니다. 그렇다면 복잡한 수학 기호는 어떻게 읽고 이해해야 할까요?
미분 기호, 이렇게 읽으세요!
어떤 함수 y를 미분했다는 표시는 보통 y’ (y 프라임)으로 간단히 표현합니다. 하지만 수학자들이 사용하는 공식적인 기호는 아래와 같습니다.
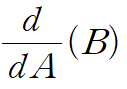
이 기호는 d/dx 와 (y)로 나눌 수 있습니다. 이것은 수학적인 약속이니, 이렇게 받아들이시면 됩니다.
d/dx: “x로 미분해라” 라는 명령어(Operator)입니다.(y): “y를” 이라는 대상(Object)입니다.
두 개를 합쳐 한국어 어순으로 바꾸면? **”y를 x로 미분해라”**라는 명확한 뜻이 됩니다.
이계도함수 기호의 의미
이계도함수는 ‘한 번 미분한 함수(도함수)를 한 번 더 미분한 것’입니다. 즉, y’을 미분하면 y”이 되는 것이죠. 이를 기호로 표현하면 아래와 같습니다.
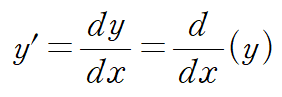
y’은 dy/dx 이므로, ‘y’을 x로 미분하라’는 의미인 $\frac{d}{dx}(y’)$는 $\frac{d}{dx}(\frac{dy}{dx})$가 되고, 이것을 줄여서 $\frac{d^2y}{dx^2}$로 표현합니다. d가 두 개, x가 두 개라서 제곱처럼 보이는 것이죠!
📈 2단계: 이계도함수의 진짜 의미 파헤치기
도함수(y’)가 ‘변화량’을 나타낸다면, 이계도함수(y”)는 **’변화량의 변화량’**을 나타냅니다. 아직 와닿지 않으시죠? 두 가지 개념으로 설명해 드릴게요.
의미 1: 가속도
이동거리를 시간에 대해 미분하면 ‘속도’가 됩니다. 그리고 그 속도를 한 번 더 미분하면 바로 ‘가속도’가 되죠. 즉, 이계도함수는 **변화가 얼마나 더 가파르게, 혹은 완만하게 변하는지**를 알려주는 척도입니다.
의미 2: 그래프의 볼록성
이계도함수의 부호에 따라 그래프의 모양이 결정됩니다. y” > 0 이면 그래프는 ‘아래로 볼록(U)’한 모양이고, y” < 0 이면 ‘위로 볼록(∩)’한 모양이 됩니다. 변곡점을 찾는 데 핵심적인 역할을 합니다.
✨ 3단계: 그래서 고계도함수는 어디에 쓸까?
우리가 편입 시험에서 고계도함수를 마주하게 되는 가장 대표적인 활용처는 바로 **테일러 급수(Taylor Series)**입니다!
지난 칼럼에서 다루었던 매클로린 급수와 테일러 급수는, 사인(sin) 함수처럼 복잡한 함수를 다항함수의 합으로 근사하여 표현하는 강력한 방법입니다. 이때 각 항의 계수를 결정하는 것이 바로 n계도함수, 즉 고계도함수입니다. 고계도함수 없이는 테일러 급수도 존재할 수 없는 것이죠.
오늘의 결론
고계도함수는 ‘여러 번 미분하는 것’이며, 그 진짜 의미는 ‘변화의 변화’를 측정하는 것입니다. 그리고 이것은 테일러 급수라는 강력한 도구를 만드는 핵심 재료가 됩니다.
“편입을 경험했기에, 합격은 튜나입니다.”
