에빙하우스 망각곡선, 그리고 편입수학 ‘누적복습’의 모든 것

[편입수학 공부법 / 누적복습 / 에빙하우스 망각곡선 / 효율적인 공부법]

🧠 우리 뇌는 왜 배신하는가? (에빙하우스 망각곡선)

혹시 위 그래프를 보신 적 있으신가요? 바로 그 유명한 **에빙하우스의 망각곡선**입니다. 독일의 심리학자 헤르만 에빙하우스가 발견한 이 곡선은, 우리가 새로운 정보를 학습한 후 시간이 지남에 따라 얼마나 빨리 잊어버리는지를 보여줍니다.

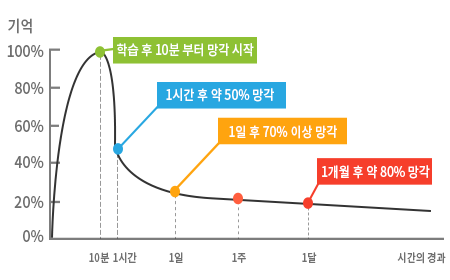
그래프가 보여주듯, 망각은 학습 직후부터 매우 빠르게 일어납니다. ‘미분’ 개념을 저와 함께 배우고 문제를 풀면, 그 순간에는 다 이해되고 혼자서도 할 수 있을 것 같은 기분이 들죠. 하지만 우리 뇌는 배운 직후 10분만 지나도 망각을 시작하고, **1시간이 지나면 방금 배운 내용의 50%를 잊어버립니다.**

이것은 여러분의 기억력이 나빠서가 아닙니다. 모든 인간의 뇌가 그렇게 설계되어 있습니다. 그리고 이 ‘망각’이라는 자연스러운 현상에 맞서 싸우는 유일하고 가장 강력한 무기가 바로 ‘복습’입니다.

⚔️ 망각과 싸워 이기는 유일한 무기, 누적복습

위 그림의 빨간색 곡선을 봐주세요. 복습을 안 하면 한 달 뒤 기억량의 80%가 사라집니다. 하지만 노란색 곡선처럼, 10분 후 짧게라도 복습하면 기억량은 다시 100%로 회복됩니다. 그리고 신기하게도, 다음 망각의 속도는 이전보다 훨씬 느려집니다.

이것이 바로 누적 복습의 힘입니다. 주기적인 복습은 단순히 잊어버린 것을 다시 채우는 행위가 아니라, **기억을 장기 기억으로 전환하고, 망각의 속도 자체를 늦추는 가장 과학적인 방법**입니다.

🎯 1%의 차이: 당신이 10회독을 해야 하는 진짜 이유

누적 복습은 쉽게 말해 ‘계속 누적해서’ 복습하는 것입니다. 저는 학생들에게 미적분이 끝나고 선형대수학을 배울 때, 그 한두 달 사이에 미적분을 적어도 3회독은 하라고 이야기합니다. 그러면 학생들은 의아해합니다. “이미 다 풀어본 똑같은 책을 왜 또 보나요?”

정말 공부를 모르는 학생들이 하는 실수가 바로 이 부분입니다. 똑같은 책을 9번, 10번 풀어봐도 늘 모르는 문제, 틀리는 문제가 발생합니다. 제 미적분 교재에는 약 1000문제가 넘게 실려있습니다. 10회독을 한 학생이라도, 그중 모르는 문제, 헷갈리는 문제는 10문제 내외로 반드시 존재합니다.

“990문제는 아는데, 그 정도면 되지 않나요?” 절대 아닙니다. 단언컨대, **시험장에서는 여러분이 아는 990문제가 아니라, 바로 그 헷갈리는 10문제가 나옵니다.** 나만 헷갈리는 문제는, 교수님들이 변별력을 위해 내기 딱 좋은 문제이기 때문입니다.

우리가 복습을 하는 진짜 이유는, 아는 99%를 확인하기 위함이 아니라, 합격과 불합격을 가르는 그 1%의 문제를 내 것으로 체화시키기 위함입니다. 그 1%의 차이 때문에 학교가 갈립니다. 똑같은 교재를 반복해서 푸는 것은 지겹고, 재미없고, 힘듭니다. 하지만 공부란 것이 원래 그런 것입니다. 그것이야말로 여러분이 제대로 공부하고 있다는 가장 확실한 증거입니다. 꼭 복습 열심히 해주세요!