안녕하세요~~
오늘은 저번 시간 벡터 공간의 이야기에 이어서
직교성(orthogonality)에 대해 말씀드리려 합니다.
직교성은 벡터 공간에서 중요하게 다뤄지는 내용이지만
미적분학에서도 정말정말 중요한 개념이예요!!
왜 이 개념이 미적분학에서도 등장하는지는 차차 말씀드리겠습니다.
선형대수의 벡터 공간에서 행공간, 열공간 등
다양한 부분공간(subspace)에 대해 말씀드렸었죠!
하지만 이러한 부본공간들은 그 각각의 의미를 아는 것도 중요하지만
각 부분공간들의 관계를 파악하는 것도 무척 중요합니다!
이러한 부분공간들의 가장 중요한 관계는 바로 직교 관계입니다!!
그래서 오늘은 이러한 부분공간들의 직교 관계에 대해 말씀드리기 전에,
공간에서의 직교성이란 무엇인지 설명드릴 계획입니다.
사실 직교, 수직, 직각 이런 단어는
여러분들이 이미 중고등학교 시절을 거치며
친숙하게 들어봤을 단어와 개념입니다.
우리가 벡터 공간이라는 새로운 공간에 대해서 공부하고 있지만,
그렇다고 기존에 존재하던 개념이 새롭게 정의되는건 아니예요!
차근차근 벡터 공간에서의 직교성에 대해 알아갑시다.
우선 우리는 벡터간의 직교에 대해 생각해봐야 합니다.
벡터 사이의 직교는 바로 그 유명한 내적(dot product)로 정의됩니다!
처… 처음 들어보셨다고요? ㅠㅠ
우리가 곱셈을 배운 뒤로 곱셈의 다양한 표기에 대해
별 생각없이 익숙하게 사용해왔을 겁니다.
보통 곱셈은 x 기호와 • 기호를 사용하고, 표기를 생략하는 경우도 많았죠.
하지만 벡터의 곱셈에서는 x 기호와 • 기호가 다른 의미를 갖습니다!!
x 기호는 외적, 그리고 • 기호는 내적이라고 부르고
의미와 계산 방법이 무척 상이한 개념이예요!
오늘 우리는 내적에 집중해 봅시다.
내적이 영어로 dot product 라고 하는 이유도, 기호가 • 이기 때문이예요.
물론 한자어 내적 그대로 inner product라고도 합니다.
두 벡터 x, y 간의 내적은 다음과 같이 정의합니다.
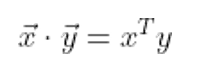
그리고, 이 내적의 값이 0이 될 때 우리는 두 벡터가 직교한다고 해요!
여기서, 분명 내적의 정의를 벡터 성분 간 곱의 합으로
그 정의를 기억하고 계신 분들도 있을거라 생각합니다.
하지만 성분 곱의 합은 위와 같은 정의에 대해서
실질적으로 계산하는 단계라는 사실을 기억해주세요!
참고로, 그럼 0벡터는 어떻게 그 직교성을 정의할까요?
수학에 있어서 0과 관련된 부분은 언제나 조심스럽게 정의하지만
내적에 있어서는 특별한 것 없이 정의에 따라,
무엇을 곱하든 0이 되기 때문에 0벡터는 모든 벡터와 직교한다! 라고 정의합니다.
그럼 이제 한 쌍의 벡터가 아닌 벡터 공간을 다시 생각해봅시다.
벡터 공간이, 특히 부분공간으로 정의된 두 벡터공간 A와 B가
서로 [직교한다]라는 말은 벡터 공간 A의 모든 벡터가
벡터 공간 B의 모든 벡터와 직교한다는 말입니다.
음… 너무 쉽고 당연한 얘기 같지요?
그럼 다음 그림을 봅시다.

쉽게 바닥과 벽면이라고 생각해보세요!
이러한 모양의 두 벡터 공간은 서로 직교하는 상태일까요?
분명 직각으로 만나고 있지만, 그림의 두 벡터 공간은 직교 상태가 아닙니다!!
어째서 그런 걸까요?
정의를 다시 한번 생각해 봅시다.
분명 우리는 ‘모든’ 벡터가 서로 직교 관계를 이루고 있어야
두 공간이 직교한다고 정의했어요.

하지만 다음과 같은 벡터를 생각해보면,
위 벡터는 두 벡터 공간 각각에 모두 속하지만
자기 자신은 자신과 직교 관계일 수가 없습니다.
(물론 앞서 말한 0벡터를 제외하고요!)
두 부분 공간이 직교하기 위해서는 우선 영벡터를 제외하고는
서로 교차되는 부분이 없어야 합니다!!
우리는 지금껏 바닥과 벽면이 서로 직교한다고 생각해왔지만,
벡터 공간의 수학적 세상에서는 그렇지 않습니다!
바로 이러한 작은 개념의 차이들이
나중에 보다 많은 개념들을 쌓아 올릴수록
점점 내용을 제대로 이해하는 것과 멀어지게 만드는 주범이예요!
오늘은 직교성의 정의와 쉽게 생각하는 오개념에 대해 다뤘는데,
다음 시간에는 이러한 직교성을 적용하여 앞서 소개해드린 벡터 공간의
각 부분 공간들 간의 관계를 정리해 보겠습니다.
그럼 다음에 또 만나요~!

