안녕하세요~!
오늘은 지난 시간에 말씀드린 대로
벡터 공간에 대해 말씀드리려 합니다.
벡터 공간은 여러분이 대학교에 와서 처음 접하게 되는
무척이나 생소한 개념일겁니다.
앗 참고로 벡터 공간은
고등학교 기하와 벡터 단원에서 배웠던 공간벡터와는
전혀 다른 개념이예요!!
단어만 보면 앞 뒤 순서만 바꿨을 뿐이기에
그게 그거 아닌가..? 라고 생각할 수 있겠지만
그 내용은 사뭇 다르답니다.
우선 고등학교 기하와 벡터에서 배운 공간벡터를 돌이켜보면
도형의 방정식과 이어지는 내용으로서
공간 속 도형을 벡터로 표현하는 방법이었습니다.
말 그대로 공간을 표현하기 위해 사용되는 벡터였지요.
하지만 벡터 공간은, 두 벡터의 선형 결합을 이용해서
새롭게 정의되며 확장되는 공간 그 자체를 나타내는 표현이예요!
참고로, 여러분이 오랜 시간 배워왔던 미적분학은
고등학교 때 개념적으로만 다뤘던 무한대, 무한소,
극한과 수렴 등등에 대해 드디어 우리가 대학에 들어오고 나서
비로소 입실론-델타 방법을 통한 수학적 정의를 배우게 됐었죠?
선형대수에 있어서도 학습 순서는 마찬가지라고 생각하시면 됩니다!
여러분은 대부분 선형대수의 개념 자체를 처음 마주하셨을 거예요.
그렇기에 대학교 공업수학에서 설명하는 선형대수는 고등학교 때
간단히 개념적으로만 이해하던 미적분학의 수준과 비슷한 수준이예요.
그래서 더욱 선형대수가, 편입 수학 부분 중 가장 손쉬운 난이도로
손꼽히는 이유입니다.
하지만 조금 더 여러분께 안심이 되는(?) 이야기를 드리자면
수학적으로 엄밀하게 전개되는 선형대수학의 심오한 이야기들은
사실 공대에 진학한 여러분은 따로 대수학 강의를 신청해 듣거나,
대학원에 진학하는 것이 아니라면 접할 일이 없을 것입니다.
그러니 선형대수 부분을 어려워하지 마시고 차근차근 그 개념들을 따라가 봅시다.
우리는 벡터 공간에 대해 간단히
두 벡터의 선형 결합으로 표현되는 공간이라고 알아 두면 충분합니다.
선형 결합은, 어떤 한 벡터에 실수를 곱해 크기를 변형할 수 있고
이러한 두 벡터를 더하고 빼는 것을 나타내는 말입니다.
그림으로 표현하면 다음과 같습니다.

그림에서 보듯이 두 벡터는 평면을 형성할 수 있습니다.
물론, 두 벡터가 평행하거나
혹은 알고 보니 두 벡터가 아닌 한 몸이었다거나
하는 불상사는 없는 경우에 한해서요.
또한 이때 중요한 조건으로
0벡터를 포함하고 있어야 평면을 이룰 수 있다는 점이 있어요!!
이러한 벡터공간의 개념 자체는 어렵지 않을거라 믿어요!
하지만 우리의 공부가 항상 그렇듯….
여기서 딱 한발자국을 더 나아가는데 거기서부터
갑자기 어려워지는 느낌입니다.
선형대수에서의 벡터공간에서는 연이어 등장하는
부분공간(subspace)의 개념이 바로 그것입니다.
부분 공간이 어렵다니, 쉬운데요?
라고 생각하는 여러분은 아마 익숙한 예로
3차원 공간과 2차원 평면을 떠올리실 거예요.
맞습니다! 바로 그게 가장 대표적인 부분공간이지요.
바로 위 그림에서 말씀드렸듯 평면은 이미 벡터공간인데,
3차원 공간은 그 평면을 포함하는 더 넓은 벡터공간이니까요.
다만 이때도 주의해야 할 것은, 항상 원점을 포함하고 있어야
벡터공간이라는 점입니다.
예를들어 사분면의 한조각은 벡터공간이 될 수 없어요!!
다시 부분공간으로 돌아와 설명하면,
부분공간의 개념이 처음 소개될 땐 다들 끄덕끄덕 쉽네 쉬워!
하고 넘어가고들 합니다.
하지만 얼마 지나지 않아서
행렬에서, 열벡터와 행벡터가 소개되고
그를 확장(span)하여 형성되는 열공간(column space)과
행공간(null space) 그리고 해공간(null space)이 등장하면
다들 또 찌그러진 개구리 페페 같은 표정이 되곤 하더라구요….

행렬과 벡터부터 간단히 시작해 볼게요.
행렬은 단순히 수를 네모 모양으로 쌓아올린 것이 아닙니다!
물론 생긴 것은 그렇게 생겼어요.
하지만 우리는 행렬을 가로로도 세로로도 쪼개어
각 벡터들의 집합으로 이루어 졌음을 이해해야 합니다.
그게 바로 행벡터와 열벡터예요.
말이 거창했을 뿐 실상은 행렬을 가로세로로 쪼개어
각각을 벡터로 생각하는 것입니다.
그럼 우리는 왜 이런 작업을 하는가? 에 대한 의문은
바로 다음 식을 풀기 위해서예요!
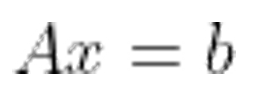
우리가 선형대수에서 계~속 공부하는 내용은 바로 이것입니다.
여기에서 A는 행렬, x와 b는 벡터입니다.
아무것도 아닌 간단한 식 같지만,
선형대수의 많은 부분을 포함하는 중요한 내용이예요.
그 중에서도 특히 행렬과 벡터의 곱이 가능하고
그 결과가 벡터로 표현된다는 부분을 이해해야 합니다.
이러한 행렬과 벡터의 곱셈을 하는 방법에는 여러 방법이 있습니다.
아마 익숙한 행벡터를 이용한 방법이 있고,
조금은 낯설 열벡터를 이용하는 방법도 있어요.
이 부분에 대한 내용은 칼럼 연재 초창기에 설명 드린 바 있으니
기억이 안나는 분은 다시금 참고해주세요!
그래프와 함께 열벡터가 어떻게 적용되는지, 설명을 드렸었는데
오늘 말씀드릴 내용은 그러한 열 벡터들의 결합으로 새로운 공간이
펼쳐질 수 있다는 얘기입니다.
말 그대로 열 벡터로 이루어진 공간이기 때문에 열공간이라고 칭하는
이 공간은, 열 벡터들의 선형조합으로 정의되는 공간이예요.
마찬가지로 행공간은 행벡터들의 선형조합으로 정의됩니다.
그리고 해공간은! 조금 전 방정식에서 b=0일 때의 공간이예요.
그럼 이 공간 들에는 무슨 의미가 있는 걸까요?
잠시 우리가 중고등학교때 배워온 방정식들을 생각해 봅시다.
일차방정식, 이차방정식, 고차방정식에서
꾸준히 매번 등장한 내용은 무엇이 있을까요?
바로 이 방정식의 해가 있느냐? 하는 것입니다.
공학에서 가장 중요한 요소는
자연 현상을 수학적 언어로 표현하고 해석하는 것입니다.
그렇게 노오력해서 결국 수학적 표현에 성공했으면!!
그 다음은 당연히 그것을 풀어서, 결과를 예측하는 것이 목표지요!
따라서 우리는 방정식을 세울 수 있는가?
그 방정식에는 해가 있는가?
라는 질문은 너무너무 중요한 질문이 되는 것이예요!
선형대수는 바로 그 질문에 대한 대답을 하기 위해서
열공간과 해공간, 그리고 부분공간의 개념을 이용한답니다.
다음 시간에는 이 내용을 독립성과 함께 설명드릴게요.
또한 이번에 잠시 언급한 확장(span)과 기저(basis)의 개념과
필요성도 말씀드리도록 하겠습니다.
안녕히계세요~~


