안녕하세요~
오늘은 지난 시간에 이어 벡터 공간에 대해 설명 드리겠습니다!
벡터 공간 부분은 각종 낯선 용어들이 등장하고
그 개념들이
호로록 지나가기 마련이라 공부할 때는 별 것 아니라고
생각할지 몰라도 나중에 개념이 헷갈리면 고생하는 단원입니다.
지난 시간 열공간과 해공간에 대해 간단하게 언급했지요.
오늘은 그 정의와 쓰임을 말씀드릴게요.
우선 벡터 공간의 확장(span)과 기저(basis)부터
시작해봅시다.
확장은 어려울 것 하나 없이 단어 그대로의 의미예요!
어떠한 벡터들이 공간을 확장한다는 말은,
그 공간을 해당 벡터들의 선형 결합으로
표현할 수 있다는 말입니다.
기저는 이렇게 공간을 확장할 수 있는 벡터들의 집합이예요.
기저들은 공간을 확장한다는 특징 외에도
서로간 독립이라는 아주 중요한 특징을 갖습니다!
가장 간단한 예로, 우리에게 익숙한 3차원 공간을 생각해봅시다.
이 3차원 공간의 가장 쉬운 기저는 x, y, z축의 단위 벡터지요!
또한 여기에서
우리가 중요하게 기억해야 하는 사실은 2가지가 있어요.
첫째는 3차원 공간의 기저는
x, y, z축의 단위 벡터가 유일한 것이 아니라는 점입니다.
x, y, z축의 단위 벡터를 떠올리며
손가락 엄지, 검지, 중지를 서로 직각으로 하고
빙글빙글 돌리면, 사실 서로 직각이기만 하면
3차원 공간을 나타내는 것에
아무런 문제가 없다는걸 알 수 있어요.
둘째는 기저인 벡터가 3개로 이루어진다는 것입니다!
3차원 공간을 이루는 기저는 첫번째에서 말씀드렸듯
그 쌍이야 다양하게 존재할 수 있지만,
그 기저를 이루는 벡터의 수는 언제나 3가지예요.
절대 2개의 벡터만으로 구성할 수도,
4개 이상의 벡터로 구성할 수도 없습니다.
보다 정확히는 4개 이상의 벡터라면
그 벡터들이 서로 독립일 수가 없어요.
이렇게 공간을 구성하는 기저 벡터의 숫자는 그 공간의 차원(dimension)이 됩니다!
이 내용들을 기억하면서 다시 행렬로 돌아와 봅시다.
우리는 오와 열을 맞춰 사각형 꼴로
정렬한 수의 덩어리를 행렬이라고 해요.
하지만 선형대수의 첫걸음은,
이러한 행렬을 벡터의 관점으로 바라보는 것입니다.
행렬의 행과 열을 각각의 벡터로 생각하는 것이 그 시작입니다.
이를 각각 행벡터, 열벡터라고 하지요.
보통 행을 기준으로 바라보는 것에 익숙할지 모르겠지만,
선형대수에서 보다
중요하게 다뤄지고 의미를 갖는 것은 열벡터입니다.
자연스레 우리는 이러한 행벡터과 열벡터가 이루는 공간을
각각 행공간과 열공간이라고 부릅니다.
물론 행렬의 구성에 따라서,
공간 자체를 만들지 못하는 경우도 있지요.
이쯤에서 우리의 목표인,
풀고 싶은 다음 식을 다시 떠올려 봅시다.
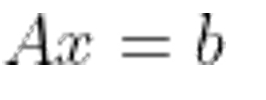
여기에서 A는 행렬이고 x는 미지수인 벡터예요.
보다 구체적으로 아래와 같은 예를 생각해봅시다.
여기에서, 열벡터가 의미하는 것은 무엇일까요?
왜 저는 열벡터가 더 중요한 역할을 한다고 했을까요?

Ax라는 행렬과 벡터의 곱은,
결국 A의 열벡터의 선형 조합이예요!!
이 말은, 곧 열공간을 뜻하게 됩니다.
A 열벡터들의 모든 선형 조합이 열공간이니까요.
이때 우리가 풀고 싶은 식 Ax=b에서,
b도 열벡터라는 사실을 잊으면 안됩니다.
결국 b가 A의 열공간안에 존재하는가? 라는 질문이
Ax=b 라는 방정식을 풀 수 있는가? 라는
질문과 같은 질문이 되는 겁니다.
열공간의 기저는 그럼 어떻게 구할 수 있을까요?
열공간의 기저는
앞서 가우스 소거법 등에서 익혔을 pivot 열이 됩니다!
이러한 pivot 열의 수를 우리는 행렬 A의 랭크(rank)라 부릅니다.
이 랭크는, 곧 열공간의 차원이기도 하지요!
이 때 주의해야 할 것은 열공간의 차원이지,
행렬의 차원이 아니라는 점입니다!
위 예시를 보면 세번째 열은 첫번째, 두번째 열의 합으로
이루어진다는 것을 볼 수 있습니다.
따라서 위 행렬 A의 랭크는 2가 됩니다.
선형대수를 처음 배우기 시작하면서 접하는 소거법들은
단순한 숫자 놀음이 아니예요.
거기에서 등장하는 pivot의 개념은 이후 벡터 공간에서
매우 중요하게 다뤄지는 개념입니다.
Pivot을 구할 수 있다면
행공간과 열공간의 차원이 같다는 것도
이해할 수 있습니다.
이러한 행공간, 열공간의 차원은
곧 영공간(null space)의 차원과도
밀접한 관련을 갖습니다.
영공간은 Ax=0 일 때를 뜻하지요!
영공간의 차원은, pivot이 아닌 free variable의 수를 뜻하게 됩니다.
따라서 자연스럽게 열공간의 차원과 영공간의 차원의 합은
행렬 A의 열의 개수가 되지요!
이렇게 행렬 A를 바탕으로 우리가 풀고
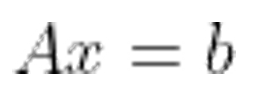
우리가 선형대수에서 계~속 공부하는 내용은 바로 이것입니다.
여기에서 A는 행렬, x와 b는 벡터입니다.
아무것도 아닌 간단한 식 같지만,
선형대수의 많은 부분을 포함하는 중요한 내용이예요.
그 중에서도 특히 행렬과 벡터의 곱이 가능하고
그 결과가 벡터로 표현된다는 부분을 이해해야 합니다.
이러한 행렬과 벡터의 곱셈을 하는 방법에는 여러 방법이 있습니다.
아마 익숙한 행벡터를 이용한 방법이 있고,
조금은 낯설 열벡터를 이용하는 방법도 있어요.
이 부분에 대한 내용은 칼럼 연재 초창기에 설명 드린 바 있으니
기억이 안나는 분은 다시금 참고해주세요!
그래프와 함께 열벡터가 어떻게 적용되는지, 설명을 드렸었는데
오늘 말씀드릴 내용은 그러한 열 벡터들의 결합으로 새로운 공간이
펼쳐질 수 있다는 얘기입니다.
말 그대로 열 벡터로 이루어진 공간이기 때문에 열공간이라고 칭하는
이 공간은, 열 벡터들의 선형조합으로 정의되는 공간이예요.
마찬가지로 행공간은 행벡터들의 선형조합으로 정의됩니다.
그리고 해공간은! 조금 전 방정식에서 b=0일 때의 공간이예요.
그럼 이 공간 들에는 무슨 의미가 있는 걸까요?
잠시 우리가 중고등학교때 배워온 방정식들을 생각해 봅시다.
일차방정식, 이차방정식, 고차방정식에서
꾸준히 매번 등장한 내용은 무엇이 있을까요?
바로 이 방정식의 해가 있느냐? 하는 것입니다.
공학에서 가장 중요한 요소는
자연 현상을 수학적 언어로 표현하고 해석하는 것입니다.
그렇게 노오력해서 결국 수학적 표현에 성공했으면!!
그 다음은 당연히 그것을 풀어서, 결과를 예측하는 것이 목표지요!
따라서 우리는 방정식을 세울 수 있는가?
그 방정식에는 해가 있는가?
라는 질문은 너무너무 중요한 질문이 되는 것이예요!
선형대수는 바로 그 질문에 대한 대답을 하기 위해서
열공간과 해공간, 그리고 부분공간의 개념을 이용한답니다.
다음 시간에는 이 내용을 독립성과 함께 설명드릴게요.
또한 이번에 잠시 언급한 확장(span)과 기저(basis)의 개념과
필요성도 말씀드리도록 하겠습니다.
안녕히계세요~~

