편린이를 위한 미적분학개론 간단 정리!

미루’s 편린이를 위한 미적분학개론 [편입 미적분학 / 편입수학 미적분학]
수학 과목의 집대성이라고 할 수 있습니다.
그만큼 적용되는 분야가 다양한 수학이예요.
미분은 변화율을 표현하기 위해 발전해왔고
적분은 넓이를 더 정확히 나타내기 위해 발전해 왔습니다.
미적분의 역사 그 자체에 대해서는
무척 흥미로운 주제지만 워낙 역사와 이야기거리가 많은 관계로
본 지문에서는 다루지 않을 겁니다.
여기서는
우리가 고등학교 수학 시간에
어떻게 미적분을 배웠는지 가볍게 되짚어 보기로 해요.
결론에 이르러서는 위에서도 말했듯
이러한 미적분이
결국
어떻게 사용되는지 말씀드리겠습니다.
여러분이
기억하는 여러분의 인생에서 미적분학이라는 것을
처음 접하게 된 것은 언제인가요?
어느 순간(!) 수학책에서 낯선 기호인
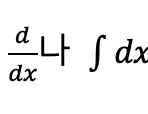
를 마주했을 때일까요?
물론 본격적으로 단원 이름에 미적분이란
단어가 쓰인 순간은 그 때가 맞겠지요.
하지만 교과 과정에서 미적분의 시발점이 되는 부분은
다름아닌 수열 단원입니다.
수학 선생님들은
여러분 몰래(?)
그때부터 미적분을 알려주기 위해
큰 그림을 그리고 있었던 거예요!
수열은 어떠한 규칙을 가지고 나열된 수예요.
대표적인 수열로 등차/등비 수열에 대해
배운 기억이 있을 것입니다.
수열에서 중요한 것은 무엇이었나요?
해당 수열의 규칙을 알고,
그를 통해 수열의 일반항을 구하는 것이었습니다.
수열 이후에는 무엇을 공부했나요?
바로 이어 수열의 극한이란 단원을 접하고
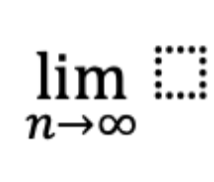
라는 기호와 극한의 개념을 처음 익혔을 것입니다.
수렴과 발산이라는 개념도요.
고등학교때 정의한 극한은
어떠한 지점을 향해 한없이 나아가는
바로 그러한 상태를 나타냅니다.
이어서 우리는 수열에서 배운 극한의 개념을
우리에게 익숙한 함수에도 적용했습니다.
함수의 극한을 통해
비로소 미분이라는 개념에 접근하게 됩니다.
이후에는 미분법이라는 이름으로
다양한 미분 방법들을 배우죠.
이공계 학생이라면 선택과목에서
초월함수의 미분에 대해서도 배우게 됩니다.
적분의 경우를 살펴보면
다양한 미분법들을 익힌 이후
곱셈 다음 나눗셈을 배웠던 것처럼
적분법을 배우게 됩니다.
적분은 구분구적법에서 시작하지요.
슬라임 같은 모양의 넓이를 구하고 싶을 때
그 넓이를 작은 도형들의 합으로 간주하여
전체 너비를 근사해 나가는 방법입니다.
이후 우리는 마찬가지로
다양한 적분법들을 익히고
초월함수에 대해서는 훨씬 복잡한 형태의
적분 공식들을 익힙니다.
그렇게 대학교에 진학하면
1학년때 대학 미적분학을 접하게 됩니다.
대학 미적분에서는
사실 엄청 낯선 미분법, 적분법이
등장하는 것은 아닙니
다.
다만 따스한 봄날의 미적분학 강의에서
고등학교때엔 위에서 말했듯이
개념으로만 얘기했던 극한을
이상한 기호들을 사용해
정의를 명확히 하고 증명한다는 것이
크나큰 차이의 시작이죠.
그렇게 조금 더 복잡한(?)
미적분학을 익히며
공업수학 강의를 듣게 되면
바야흐로 미분방정식이 등장합니다.
여기까지 참 오래 걸렸습니다.
사실 여러분이 지금껏
미적분학을 공부한 이유는
단적으로 이 미분방정식을 풀기 위함입니다.
‘미적분은 적용되는 범위가 무척 넓단다~.’
라는 말은 고등학교 때도
분명 들어는 봤을 것입니다.
수능 문제를 보더라도
매번 애꿎은 물통에 구멍을 내고
그 구멍을 막기보다
구멍에서 물이 빠져나가는 시간을
변태같이 식으로 표현하고 있지요.
변화하는 자연현상을
수학적으로 표현해 내는 것.
그것이 바로 미분방정식입니다.
예를 들어,
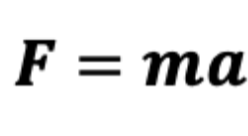
로 유명한 뉴턴의 운동식도
우리가 중학교때부터 배워왔기 때문에
쉽게 나타낸 것이지
뉴턴이 사용한 표현식은
가속도에 대한 미분방정식이었습니다.
우리는 대상을 미분방정식으로
표현하고자 노력하는 것입니다.
그리고 나서야 비로소 그 다음
해당 미분방정식을 특정 상황들에 대해 풀어내는 것이지요.
우리는 이렇게 미적분학을
오랜 시간 배워 나가며
어느덧 기계처럼 미적분 문제를 풀 수 있지만
미적분의 의미에 대해서는
잊어버리곤 합니다.
당장 눈 앞의 미적분 문제를
빠르고 정확하게 풀어내는 것이 중요하니까요.
시험을 앞둔 우리는
당연히 미분법/적분법에 익숙해져야 하지만
사실 도대체 미적분을 실제로는 어떻게 사용하는지,
왜 필요한 것인지, 다시한번 생각해보는 것이 중요합니다.


