#3. 선형대수학
안녕하세요?
이번 시간에는
선형대수학에 관련된 이야기를 해볼까 합니다.
미적분학은 분명 이름만큼은 익숙하게 들었겠지만
선형대수학이란 이름은 낯설지 않을까 싶어요.
그렇지만,
수학적으로는 미적분학과
견주어도 손색없는
무척x100 중요한 부분입니다.
공대 어느 학과를 진학해도 필수적으로 사용할거구요.
개론
그렇지만 공업수학 수업에서 등장하는 선형대수 내용은
방대한 선형대수의 내용을 얕게 다루고 있기 때문에
편입 수학을 준비하는 학생들 입장에서도
별 내용은 없는 것 같고 다소 생소해서 어렵지만
결국은 외울 것만 많은 단원으로 치부되기 일수입니다.
그런 모습을 볼때마다 마음이 아파요. ㅠㅠ
대부분의
공대에서는 [선형대수] 라는 전공 과목을
따로 개설해 가르칩니다.
3학점으로 1학기 혹은 2학기 분량의 강의가 되곤 하지요.
그만큼 이후 전공 과목을 이해하는데 있어
미적분만큼이나 필수적인 수학 지식이예요!
우선 선형대수학은
행렬과 벡터의 표현이 주가 되는 수학입니다.
지난 교육 과정 까지만 해도 고등학교 수학에서
[행렬]이라는 큰 과목이 있었어요.
무려 문과 학생들도 공통으로 배우는 범위였지요.
하지만 이 [행렬] 단원은
교육 과정의 개편으로 삭제되었습니다.
글의 시작부터 선형대수가 그렇게 중요하다고 하더니,
고등학교 수학에선 왜 없애 놓은 걸까요?
심지어 미적분학은 지난 글에서 말씀드린 바와 같이
수열부터 시작하는 대장정을 거쳐 가르치는데요.
그 이유는 제대로 활용할 수가 없었기 때문입니다.
앞서 말했듯 행렬은 문과도 함께하는
공통과정에 있었습니다.
하지만 벡터는 그 시절에도 지금도
이과의 선택과목 속에서만 존재하는 개념이지요.
바로 여기에서 문제가 생긴 겁니다.
행렬의 기본적인 성질만을 알려줄 뿐이기에
행렬이 곧 벡터의 또다른 표현 방법이라는 것과
그를 이용한 선형대수로의 이야기를 할 수 없었던 것이죠.
그래서
기존 수능 시험에 등장하는
행렬 단원의 문제는
행렬의 성질을 이용해 ㄱ,ㄴ,ㄷ 중
맞는 것을 고르는 식의
고난이도 문제가 출제되기 일수였고,
수학적으로 이후의 내용과 연결점을 제공하지 못한 나머지
행렬은
고등학교 수학에서 그 자취를 감추게 되었습니다.
그래서 결국 우리는 공업수학 과목에 이르러
선형대수 단원 속에서 행렬과 벡터를 같이 접하게 됩니다.
그래서, 결국 행렬도 벡터도 각각 들어는 봤는데
그게 선형대수랑 무슨 상관이냐구요?
이 얘기를 위해 우리가 초등학교 때 풀어본
간단한 연립방정식을 떠올려 봅시다.
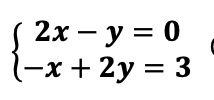
이러한 연립방정식이 있어요!
이 연립방정식을
변수들의 계수로 이루어진 행렬 A와
변수 벡터 x로 이루어진 Ax=b 라는
꼴의 식으로 표현해보면
다음과 같습니다.
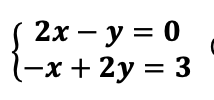
사실 여러분은 이 연립방정식을 푸는 방법을
두가지나 알고 있습니다.
그리고 여기에서 새로운 한가지를
더 소개해 드리겠습니다.
첫번째 방법은 소거법입니다.
두번째 식에 2를 곱해 첫번째 식과 더하면 변수가
사라지고 변수의 값을 쉽게 구할 수 있지요.
두번째 방법은 우리에게 너무나 익숙한 관점인,
가로로 식을 바라보는 관점입니다.
말이 어렵지만, 결국 위아래 두식으로 생각한다는거죠.
이러한 관점에서의 풀이는 어떤 것일까요?
어렵지 않습니다.
각각의 방정식은 x-y평면상에서의 직선으로 나타낼 수 있으니
두 직선의 교점을 구하면 됩니다.
바로 이렇게 말이지요!

편입 선형대수학 [편입 선형대수학 / 선형대수학]
자, 그럼 선형대수를 시작해봅시다.
이제 우리에게 중요한 것은 지금까지의
행-을 기준으로 바라본 식이 아니라
열-을 기준으로 하는 선형 조합입니다.
이 또한 말이 어렵지만, ‘x-y로 이루어진 식’이 아니라
‘각각의 변수 x와 y에 대한 조합’으로 바라본다는 말이예요.

, 이렇게 말이지요!
이러한 관점에서 바라보는 평면은 다음과 같습니다.

편입 선형대수학 [편입 선형대수학 / 선형대수학]
붉은 벡터가

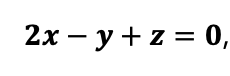
, 이와 같은 식을 우리는 뭐라고 불렀었나요?
기하와 벡터를 공부하신 학생은 기억해줬으면 해요(..).
바로 평면의 방정식입니다.
x, y, z로 이루어진 방정식이 3개 있다면
3개 평면의 교점이 구하고자 하는 해가 됩니다.
하지만 선형 조합을 통해서는 계속해서 벡터들의 합으로 표현되지요.
심지어 변수가 더 늘어나면 3차원에 사는 우리는
더 이상 그래프의 형태로 표현할 수조차 없습니다.
행렬과 벡터의 곱으로 이루어진 선형 조합으로
방정식을 새롭게 해석하는 것이 선형대수학의 시작입니다!
선형대수가 이런 방식으로 시작하는구나~ 라는걸
알아줬으면 해요!
다음 시간에는 그래서 결국 선형대수를 배우는 목표가 무엇인지에 대해
이야기 해볼게요.



