안녕하세요~!!
오늘은 지난 시간에 이어
미적분학의 기본 원리를 마무리 지어볼게요!
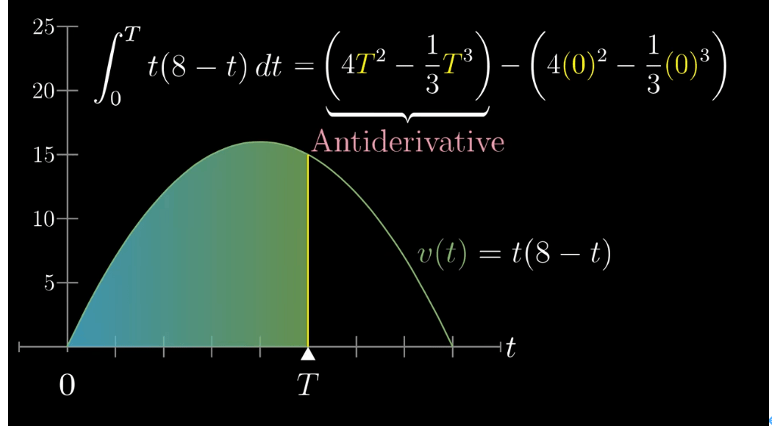
지난 시간 마지막 설명 부분의
속도 그래프와 누적 이동거리 함수가 기억 나시나요?
시간에 대한 속도의 그래프 v(t)를 바탕으로
임의의 시간 T에 대해서
시간 T까지의 누적 이동거리를 나타내는 함수 s(T)를
구하는 방법을 통해
미적분의 기본 원리를 말씀드리겠습니다!
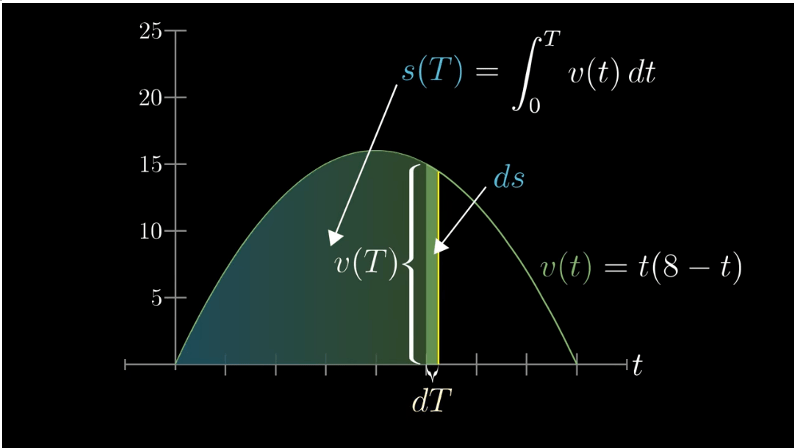
시간 구간을 잘게 나누어 넓이를 근사했던
지난 시간의 방법과 비슷한 내용이예요!
우선 작은 시간간격 dT 동안의 이동거리를 위 그림처럼
ds라고 정의합니다.
속도는 이동거리를 이동 시간으로 나누어 표현되므로
우리는 ds/dT = v(T) 라 할 수 있죠!
이 말은 곧,
무언가 모르는 함수를 미분했더니 v(t)가 됐다는 얘기예요!
우리는 결국 미분의 역과정을 통해 모르는 함수를 찾게 됩니다.
그렇지만 상수항은 미분하면 사라지게 되므로
우리는 미분의 역과정으로 구한 함수에,
구하고자 하는 이동거리의 시발점이었던
T=0을 대입하게 됩니다.
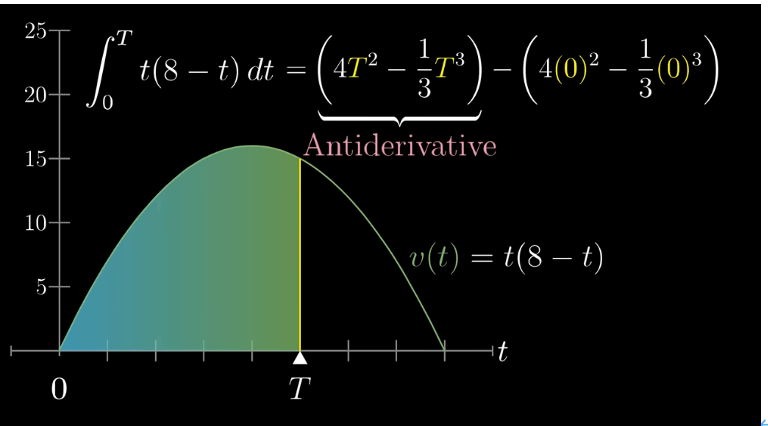
정리하면, v(t)를 적분하여
시간 T 까지의 이동거리를 구하는 문제는
위와 같이 풀이할 수 있어요!!!
여러분은 분명 이러한 과정 자체는
무척이나 익숙하실 겁니다.
하지만, 이러한 과정 자체가
미적분의 기본 원리예요!
미분 과정의 역으로서 적분이 정의되는 과정이기도 하고요.
여기에서는 간단히 앞으로만 이동하는 속도 그래프를 사용했지만,
그래프의 위치가 음/양을 넘나들어도 상관없다는 것도
이미 알고 계시겠죠?!
속도 그래프가 음수인 경우의 이동거리는
기존 이동 거리의 반대 방향으로 이동했다! 란 의미일 뿐입니다.
수학을 공부하면서 우리는 쌍을 이루는 연산을 계속해 배워왔어요.
덧셈과 뺄셈, 곱셈과 나눗셈부터 시작해서
지수와 로그도 빼놓을 수 없죠!
미분과 적분도 마찬가지랍니다.
항상 뒤에 배운 역연산이 조금 더 어려웠을 거예요.
특히나 미적분에 이르러서는
적분하는 것 자체가 도전인 그런 경우가 많습니다.
따라서 우리가 편입 수학에서 마주하는 적분법들은
능숙하게 다룰 수 있어야 해요!
신기하게 생긴 함수를 마주하더라도
기존에 배웠던 어떠한 적분법을 사용하면
적분이 되는지를 파악하는 것이 중요하답니다.
오늘은 미적분학의 기본 공식에 대한 설명을 마무리 지었고,
다음 글에서는 미적분이 겹쳐서 여러 번 등장하게 되는
고계도함수에 대해 설명 드릴게요!
감사합니다.








