편린이를 위한 편입수학 다변수함수 다중적분 / 세부단원별 공부해야할 포인트정리! [미루’s 편입수학/독학편입/편입수학컨설팅]

안녕하세요~
오늘은 지난 시간에 이어서 다변수함수에서의
다중적분에 대해 말씀드리겠습니다!
미분과 적분의 관계와 마찬가지로
이것도 편미분에 대한 역연산 아니냐?! 라고 짐작하셨다면
개념적으로는 물론 맞는 생각이예요!!
다중적분도 지난 시간의 편미분과 같이
다변수함수에서 이루어지는 적분 계산 방법입니다!
하지만 지난 시간,
다변수함수에 대한 기하학적 접근과 그에 대한
접평면등의 편미분 개념은 그렇게 중요하지 않다고 말씀드렸었죠.
중적분에서는 3차원 그래프를 제법 보실 수 있습니다.
정말 기상천외하게 생긴 오만가지 도형과 그래프에 대해
실질적인 부피를 구할 수 있는 중요한 방법이거든요!
기존 일변수함수에서의 도형의 부피를 구하는 문제에서는
회전체 문제가 자주 등장했죠.
하지만 이제 중적분을 익힌 여러분은
회전체가 아닌 괴이한 형태의 3차원 물체들 부피를 구할 수 있게 됩니다!!
그럼 z=f(x,y) 함수에서 다중적분을 적용 해볼게요.
이 함수의 그래프를 상상해보면,
x-y-z 세 축으로 이루어진 3차원 공간에서
어떠한 부피를 차지하고 있는 도형입니다.
미적분의 기본 정리를 말씀드릴 때,
작은 직사각형들의 합으로 넓이를 표현하는
적분의 개념에 대해 설명 드렸었죠?
이러한 개념의 차원을 확장시켜 3차원 공간에 도입해보면
우리는 작은 직사각형의 넓이 대신 작은 막대기의 부피를
생각해 볼 수 있습니다.
아래 그림을 보시면 이해가 쉬울 거예요!
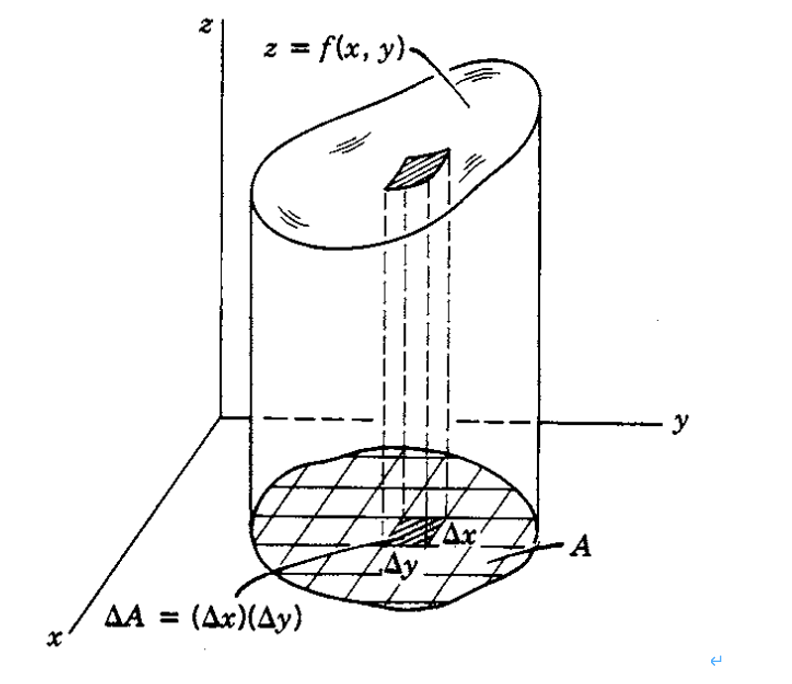
작은 미소길이 dx에 대한 직사각형의 넓이의 합으로
계산되었던 적분과 마찬가지로
작은 미소부피 dxdy에 대한 막대기의 부피의 합으로
중적분을 표현할 수 있습니다.
이 때, 중적분에서 가장 중요한 것은
적분 구간과 순서의 설정입니다!!
적분은 항상 구간에 대해 그 값을 계산할 수 있습니다.
일변수함수에서의 적분 구간은
구하고 싶은 범위가 직관적으로 보이기 마련입니다.
하지만 다변수함수에서의 적분 구간은
해당 변수에 따라 관점을 다르게 설정해야 합니다.
마찬가지로 적분 구간과 해당 변수의 매칭이 잘 되었는지
꼼꼼히 살펴봐야 합니다.
이는 곧 적분 순서가 제대로 되어 있는지를 확인하는 것입니다.
위에 예를 들었던 잘린 원기둥을 다시 가져와 보겠습니다.
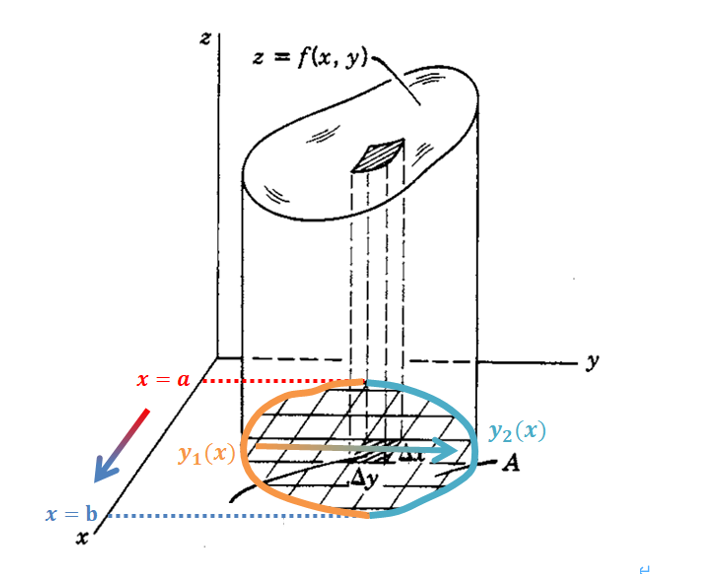
잘린 윗면을 x-y 평면에 정사영 했을 때,
x축에서의 범위는 a에서부터 b까지,
y축에서의 범위는 y1(x)에서부터 y2(x)까지입니다.
일변수함수의 정적분에서 우리가 x를
a에서부터 b까지 바꿔가면서 그 합을 계산했다면,
중적분에서는 x는 a에서 b까지 쌓여가고,
y는 y1(x)에서부터 y2(x)까지 쌓여간다고 생각하시면 됩니다!
이것을 식으로 나타내면 다음과 같죠.
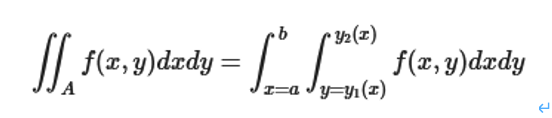
사실 여기에서 y의 범위 식이 x에 대한 함수로 이루어져 있기 때문에
중적분을 일반적인 적분으로 바꾸어 풀어낼 수 있습니다!
일반적인 예를 들어 설명 드렸지만
주어진 문제에 따라서 중적분의 적분 순서를
결정하는 것은 정말 중요합니다!
같은 문제라 하더라도
x부터 적분을 해 나아갈지,
y부터 적분을 해 나아갈지 선택에 따라서
적분 과정의 난이도가 달라질 수 있거든요.
식에 따라 위의 예시에서 마지막에 말씀드린 것처럼
적분 범위가 하나의 변수로 표시되어
정리하면 일반적인 일변수함수의 정적분 계산으로
바뀌어 버리는!! 경우도 있습니다.
다중적분 문제는 편미분과 달리
이렇게 실질적인 도형의 부피를 구하는 문제가 많이 나옵니다.
적분의 순서와 범위에 유의하며 풀어나가면
어렵지 않을 거예요!
다음 시간에는 테일러급
수에 대해 설명드릴게요~
감사합니다!








