편린이를 위한 편입수학 고계도함수 / 세부단원별 공부해야할 포인트정리! [미루’s 편입수학/독학편입/편입수학컨설팅]

안녕하세요~
앞으로는 편입 수학에서 다루는 미적분학 뒷부분에 대한
이야기를 해볼 거예요!
그 중에서도 오늘은 미분이 중복해서 나타나는
고계도함수에 대해 말씀드리겠습니다.
특별히 새롭거나 어려운 내용은 전혀 없습니다!
정말 간단하게 한마디로 정리하면
해당 변수에 대해 여러 번 미분을 수행해 주면 됩니다!!
무척이나 간단한 이야기지요!
하지만 단순히 미분 계산을 여러 번 하기 앞서,
고계도함수의 의미와 함께
고계도함수를 우리가 편입 시험에서 언제 볼 수 있는지
정리해 보도록 하겠습니다.
가장 간단한 고계도함수인 이계도함수부터 살펴봐요.
도함수는 변수의 변화에 대한 함수의 변화량을 나타내는 함수였죠?
이계도함수는 변화량의 변화량을 나타내는 함수입니다!
역시 바로 이렇게 정의만 듣고 나서는 무슨 얘기인지
와 닿지 않으실 거예요.
그러면 이계도함수의 수학 기호부터 다시 살펴보도록 합시다.
함수 f(x)에서 x에 대한 이계도함수는 다음과 같이 표현합니다.
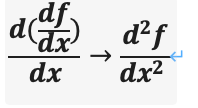
천천히 그 의미를 살펴보면 분자의 df/dx는
기존 우리가 알고 있는 바로 그 도함수예요.
이러한 도함수를 다시 x에 대한 변화량의 관점에서
살펴본 것이 이계도함수입니다.
이계도함수의 수식에서
사실 분모 부분은 (dx)의 제곱으로 표현되어야 하겠지만,
x에 대해 두 번 도함수를 취했다는 내용이 중요한 것일 뿐이라
편의상 괄호를 생략하기로 한 것이예요.
변화량의 변화량이라는 와 닿지 않는 말에 대해서
그림을 통해 표현하면 다음과 같습니다.

첫번째 dx라는 시간 변화량 동안의 함수 변화량은 df1,
두번째 dx라는 시간 변화량 동안의 함수 변화량은 df2라 했을 때
이 두 함수 변화량 간의 차이가 d(df)가 되는 겁니다.
그리고 이 변화량의 차이를 (dx)의 제곱에 대한 비로 나타내게 됩니다!
이러한 고계도함수가 적용되는 개념은 무엇이 있을까요?
실생활에서 자주 등장하는 것은 이동거리-속도-가속도로 이어지는
시간에 따른 이동 관련 함수들이지요!
하지만 우리가 편입 시험에서 주로 마주하게 되는 활용예는
바로 테일러급수입니다!
물론 이와 연관되는 라플라스, 푸리에 변환은 물론이고요.
테일러급수는 고계도함수의 합을 통한 근사식으로,
사인 함수와 같은 형태의 함수를
다항함수의 합으로 표현해 낼 수 있는 방법입니다!
테일러 급수에 대해서는 다음에 더 자세히 말씀드릴게요.
오늘은 고계도함수에 대해 설명드렸어요!
다음 시간에는 다변수함수에서의
편미분과 중적분에 대한 내용을 말씀드릴게요!!
감사합니다~

