편입수학 벡터공간 완벽정리!

안녕하세요?!
지난 시간까지 주로 미적분에 대한 얘기를 했었죠!
공업수학에서 다루는
미적분의 가장 큰 목표는
다름아닌 미분 방정식을
이해하고 풀어내기 위해서 였고
라플라스 변환의 방법을 이용해서
복잡한 초월함수들이 들어간,
또는 고계도 미분 방정식도
대수적으로 쉽게 계산할 수 있다는 것을
말씀드렸어요!
칼럼 초반에,
선형대수 단원에 대해서도 정리해
말씀드린 적이 있지만
오늘은 그 때 미처 다루지 못했던 선형대수의
다른 부분들에 대해 이야기하려 합니다.
다시금 말씀드리지만,
선형대수학도 사실 공대의 수학에서
미적분학 못지않은 위치를 차지하는 수학 분야입니다.
선형대수학에서 우리가 배울 수 있는 것을
다름아닌 행렬과 벡터의 계산이 전부가 아닙니다.
가장 중요한 것은 공간의 확장이예요.
그리고 그 이후 그러한 벡터 공간의 특성을 표현하기 위해
고유값과 고유벡터 등의
개념이 등장하고 특이점분해(SVD)등의
내용으로 이어지게 됩니다.
하지만 사실 선형대수와 미적분학은
그 둘이 따로 쓰이기보다는
으레 수학 개념들이 언제나 그래왔듯,
서로서로의 개념들을 함께 사용되는 경우가 더 많습니다.
간단한 미분 방정식을 예로 들어볼까요?
다음과 같은 미분 방정식이 있어요.
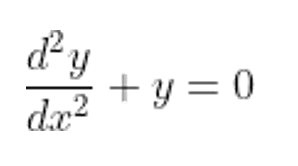
열심히 미적분학을 공부하신 여러분들이라면 보기만 해도
바로 눈으로 답이 구해질 정도로 간단한 문제입니다 😊
특수해는 바로 cos(x) 혹은 sin(x)가 되겠지요!
이를 바탕으로 상수항과 함께 일반해를 표현하면 다음과 같이 됩니다.
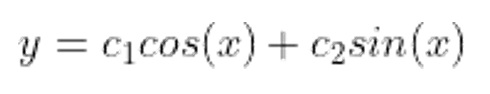
여기에서, 말씀드리고 싶은 것은
이러한 미분 방정식의 일반해의 표현이
곧 벡터 공간이라는 것입니다!!
해당 예제에서의 일반해는 곧
사인과 코사인을 기저로 하는 해공간이 됩니다!
해당 공간의 차원은 이계도 함수로 이루어진
미분 방정식이니 2가 되겠죠.
물론, 예로 든 미분 방정식의 해공간의 기저는
사인과 코사인 뿐 아니라
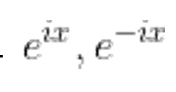
이런 녀석들도 가능합니다.
하지만 여러분은 분명 뭔가 의아한 느낌이 들겁니다.
선형대수를 통해 벡터와 행렬을 배웠다고 생각했는데,
아무리봐도 방금 제가 벡터 공간의 기저라고 말한 사인,
코사인은 지금껏 함수로 알고 계셨을테니까요.
물론 함수가 맞지요!
하지만 사인과 코사인, 이 둘을 보시면 선형 결합이 가능합니다!
‘일반해’로 알고 있는 표현이 선형 결합과
똑 같은 표현이라는 것이 보이시나요??
그렇기에
삼각함수 벡터로 취급하면서 벡터 공간의 개념을
확장해 낼 수 있는 겁니다.
이렇듯 전혀 별개의 단원이라고 생각하고 계시겠지만
선형대수와 미적분학도 많은 부분이 서로 연관이 있어요.
여러분이 전자전기, 컴공 등의 학과에 진학하신다면
선형대수와 미적분학의 보다
화려한 어우러짐을 느끼실 수 있겠지만
그건 성공적인 편입 이후의 과정일 테니
벌써부터 겁먹지 마시길 바랍니다.
다행히도 편입수학에서는 선형대수라는 과목이
가장 기초적인 행렬과 벡터의 소개부터 시작하고
이러한 미적분학과 연계되는 부분이나,
선형대수의 특이값분해와 같은 내용들은 등장하지 않아서
전체적으로 선형대수 부분의 문제 난이도가 낮은 편이예요!
미적분학 쪽과 연관되는 내용도 전혀 없다시피 하기에
사실상 뭔가 중간에 쉬어 가는 느낌으로? 배우곤 하지요.
하지만 위에 예로 들었던 문제에서도 언급된
벡터 공간의 개념과 관련된 문제들은
언제나 단골 기출 단원 중 하나라고 할 수 있습니다.
앞으로는 이러한 벡터 공간의 개념과 확장에 대해
말씀드리려 해요.
그리고 이어서 행공간, 열공간 등의 개념도 소개드릴게요.
행공간, 열공간, 그리고 앞서 예제에서 제가 언급한 해공간 등등
사실 이러한 벡터 공간들은 서로 긴밀한 관계가 있어요!
이 단원들의 내용 자체는 그렇게 어렵지 않지만,
수학적으로 무척 생소한 개념이 등장하는 단원이고
이후 계속해서 다뤄지는 내용입니다.
제대로 이해를 못하신 채로
선형대수는 내용도 별로 어렵지 않고
열심히 암기만 하면 된다고 했어!!! 라고 생각하시다가는
선형대수의 절반을 손해보시는 거라 생각해요 ㅠㅠ
자세한 이야기는 다음 시간부터 말씀드릴게요!
편입 수학의 범위를 넘어서는 부분이 있다면
미리 말씀드리면서 최대한 쉽게 설명드릴 수 있도록
준비하겠습니다.
감사합니다~!








