수학공부가 아닌 편입수학공부를 하자
많은 학생 분들이 편입수학을 시작할 때 혹은 공부할 때 범하는 실수들이 있습니다.
가령 미적분을 배울 때 고등학교 내용과 많이 겹치다보니 고등학교 때 문제를 푸던 습관 혹은 문제풀이 방식을 기억해내서 편입수학에 적용 하려는 학생들이 꽤나 많다는 것이죠.
하지만 이는 매우 좋지 않은 공부방법입니다. ㅠㅠ 분명 수학은 세계 어디에서나 일맥상통하는 엄청난 학문임은 맞지만 저희는 수학자가 아니라는 것을 항상 생각해 주셔야 합니다.
저희는 입시라는 시험을 준비하는 입시생입니다.
따라서 각 입시 시험별로 원하는 방향성이 존재를 하고, 또한 입시생들은 좋든 싫든 그 시험을 치기로 마음먹었다면 합격하기 위해서 반드시 정해진 방향성을 따라 가야합니다.
즉 수능이라는 입시시험이 원하는 방향에서의 문제풀이와 편입이라는 입시시험이 원하는 방향에서의 문제풀이는 분명히 다르다는 것 이죠.
음.. 무슨 소린지 싶으실 수 있기 때문에 한 가지 예를 들어드리겠습니다!!
가령 미적분을 배울 때 고등학교 내용과 많이 겹치다보니 고등학교 때 문제를 푸던 습관 혹은 문제풀이 방식을 기억해내서 편입수학에 적용 하려는 학생들이 꽤나 많다는 것이죠.
하지만 이는 매우 좋지 않은 공부방법입니다. ㅠㅠ 분명 수학은 세계 어디에서나 일맥상통하는 엄청난 학문임은 맞지만 저희는 수학자가 아니라는 것을 항상 생각해 주셔야 합니다.
저희는 입시라는 시험을 준비하는 입시생입니다.
따라서 각 입시 시험별로 원하는 방향성이 존재를 하고, 또한 입시생들은 좋든 싫든 그 시험을 치기로 마음먹었다면 합격하기 위해서 반드시 정해진 방향성을 따라 가야합니다.
즉 수능이라는 입시시험이 원하는 방향에서의 문제풀이와 편입이라는 입시시험이 원하는 방향에서의 문제풀이는 분명히 다르다는 것 이죠.
음.. 무슨 소린지 싶으실 수 있기 때문에 한 가지 예를 들어드리겠습니다!!
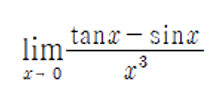
이라는 문제가 있습니다.
문과 이과의 구별 없이 극한문제에서 모두들 알고 있는 공식이 있죠!!
바로 로피탈 공식입니다! 위 식에 로피탈을 적용해보면
문과 이과의 구별 없이 극한문제에서 모두들 알고 있는 공식이 있죠!!
바로 로피탈 공식입니다! 위 식에 로피탈을 적용해보면

미분하는 계산과정을 많이 생략하긴 했지만 미분 할 때 곱미분이 계속 사용되기 때문에 실수할 가능성이 높아집니다.
여튼 3번이나 로피탈을 해서 어렵게 구한 위 식에 0을 대입하면 1/2 이라는 답을 도출하게 됩니다!!
그런데 이렇게 미분도 어렵고 계산도 오래 걸리는 문제를 왜 낼까요??
수능에 나왔다면 100분이라는 시간을 잘 활용해 보라는 의미이겠고 내신시험에 나왔다면 1등급을 가리기 위한 변별력 문제이겠죠.
그러나 편입시험에 위 문제가 나와, 로피탈을 사용해서 이 문제를 풀게 된다면 정말로 잘못된 풀이 방법입니다.
편입시험은 대학교 3학년으로 들어가는 시험인 만큼 1,2학년에 수강했어야 할 과목들을 알고 있는지를 시험해 봐야겠죠??
따라서 1,2학년때 배운 방식으로 이 문제를 풀어봐라 하고 문제를 낸 것입니다.
그래서 어떻게 푸는거냐??
해답은 공식 암기와 답 암기입니다!!
위 문제는 1,2학년 때 배우는 ‘매클로린 급수’를 사용하면 미분 할 필요도 없이 20초안에 풀이가 가능하며 단순 공식이기 때문에 풀이를 쓸 것도 없습니다.
한 술 더 떠서 위 문제는 워낙 많이 시험에 출제되었고 앞으로도 충분히 나올 수 있기 때문에 그냥 답 자체를 외워버리는 것이죠!!
즉 1,2학년 수준의 지적능력, 암기능력, 문제풀이 속도와 순발력까지 모두 보고 판단하는 시험이 바로 편입시험입니다.
물론 학생들께 이렇게 말하면 에이 그게 무슨 수학이에요.. 답을 암기하라뇨…
이런 반응이 나오지만 우리는 편입을 준비하기 때문에 편입시험이 원하는 방향성을 반드시 따라가 주어야 합니다!!
편입수학 중 제일 처음으로 배우는 미적분부터 틀린 방향성을 가지고 공부를 해나간다면 앞으로 있을 선형대수, 다변수, 공수 모두에서 무너지게 되겠죠.
이점을 항상 유의하시고 자기가 올바른 방향으로 가고 있는지를 항상 의심하며 입시생활을 하시는 것을 당부하고 싶습니다!!
수학공부가 아닌 편입수학 공부를 하자!!
여튼 3번이나 로피탈을 해서 어렵게 구한 위 식에 0을 대입하면 1/2 이라는 답을 도출하게 됩니다!!
그런데 이렇게 미분도 어렵고 계산도 오래 걸리는 문제를 왜 낼까요??
수능에 나왔다면 100분이라는 시간을 잘 활용해 보라는 의미이겠고 내신시험에 나왔다면 1등급을 가리기 위한 변별력 문제이겠죠.
그러나 편입시험에 위 문제가 나와, 로피탈을 사용해서 이 문제를 풀게 된다면 정말로 잘못된 풀이 방법입니다.
편입시험은 대학교 3학년으로 들어가는 시험인 만큼 1,2학년에 수강했어야 할 과목들을 알고 있는지를 시험해 봐야겠죠??
따라서 1,2학년때 배운 방식으로 이 문제를 풀어봐라 하고 문제를 낸 것입니다.
그래서 어떻게 푸는거냐??
해답은 공식 암기와 답 암기입니다!!
위 문제는 1,2학년 때 배우는 ‘매클로린 급수’를 사용하면 미분 할 필요도 없이 20초안에 풀이가 가능하며 단순 공식이기 때문에 풀이를 쓸 것도 없습니다.
한 술 더 떠서 위 문제는 워낙 많이 시험에 출제되었고 앞으로도 충분히 나올 수 있기 때문에 그냥 답 자체를 외워버리는 것이죠!!
즉 1,2학년 수준의 지적능력, 암기능력, 문제풀이 속도와 순발력까지 모두 보고 판단하는 시험이 바로 편입시험입니다.
물론 학생들께 이렇게 말하면 에이 그게 무슨 수학이에요.. 답을 암기하라뇨…
이런 반응이 나오지만 우리는 편입을 준비하기 때문에 편입시험이 원하는 방향성을 반드시 따라가 주어야 합니다!!
편입수학 중 제일 처음으로 배우는 미적분부터 틀린 방향성을 가지고 공부를 해나간다면 앞으로 있을 선형대수, 다변수, 공수 모두에서 무너지게 되겠죠.
이점을 항상 유의하시고 자기가 올바른 방향으로 가고 있는지를 항상 의심하며 입시생활을 하시는 것을 당부하고 싶습니다!!
수학공부가 아닌 편입수학 공부를 하자!!
